It feels safe to say that the oscillator is the core of the typical synthesizer: the actual source of fluctuation, the actual voice that provides the foundation on which sounds are built. And while the oscillator provides the structural bedrock of most sound, much of a synthesizer's sonic identity often comes from another section altogether: the filter.
For many synthesizers, the filter is one of the most identifiable parts of the sound. Depending on the filter's settings, even a single synth can change from sounding smooth and liquid to grinding and aggressive—and moreover, the character of one brand or model of filter can be dramatically different from others. After all, the sound of the Minimoog is quite different from the sound of an ARP Odyssey: and the filter is a huge reason why.
Filters have the capacity to dramatically transform simple sounds, and being familiar with their various forms and techniques provides the potential for powerful sound design.
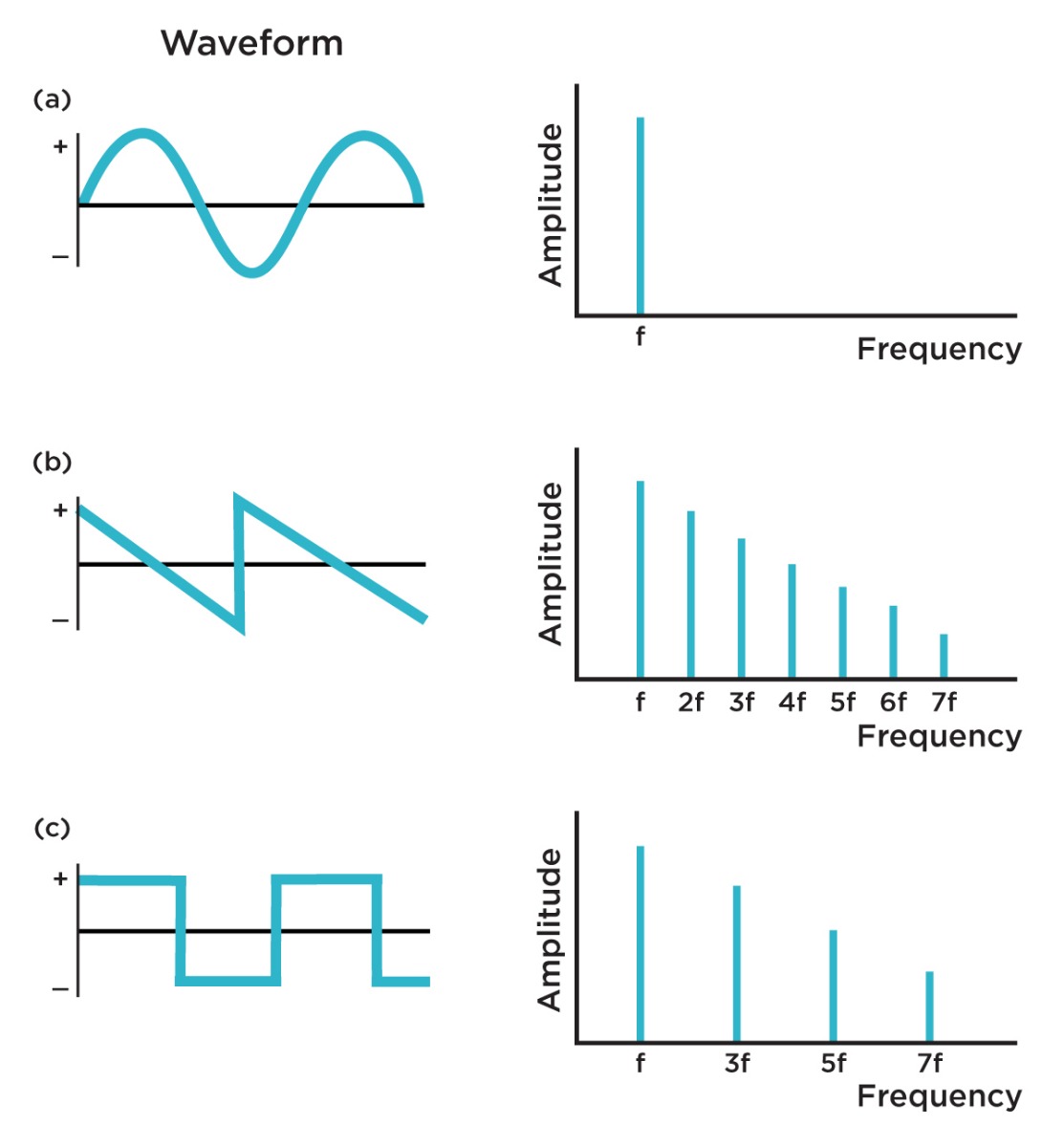Waveshapes and spectral content for: a) Sine wave; b) Saw wave; c) Square wave
What is Subtractive Synthesis?
Synthesis in general can broadly be understood as the creation and modification of sounds for creative purposes. Some of the first electronic instruments that we might now label as synthesizers emerged in the 1960s from the minds of pioneers such as Bob Moog and Don Buchla. Both designers created remarkably similar modular approaches to instrument design, each centered around similar building blocks. For both designers, the key starting point for creating a sound was generally an oscillator: a device that produces a constant tone. Both Moog and Buchla's oscillators had the capability of producing a variety of different timbres, themselves—including basic waveshapes such as sine, sawtooth and square waves.
By their nature, each waveshape has different harmonic content—the reason that we are able to perceive the difference between a saw wave and a square wave, for instance, is because of the difference in their harmonic structure: the structure of overtones, higher pitched tones internal to a sound, usually tuned to direct multiples of the perceived fundamental pitch. Some wave shapes are rich in harmonic structure (saws and squares fall into this category), while others are weaker (triangles, for instance). And ideally, a sine wave should have no harmonic content aside from its pure fundamental pitch. Of course, these raw waveshapes are quite static and generally do not offer much musical interest in and of themselves.
In both Moog and Buchla's instruments, one of the primary ways of modifying these raw sounds involved using Voltage-Controlled Filters (VCFs). Filters are devices that provide the potential to limit the loudness of certain parts of the audio spectrum—that is, they offer the ability to reduce the volume of certain harmonics present in a sound. When fed a sound with a rich harmonic structure (again, such as a saw or square wave), filters can remove specific ranges of the spectrum in order to create new sounds. This technique is commonly referred to as subtractive synthesis, since it hinges on the idea of removing energy from certain frequency ranges of harmonically rich sounds. This method provides musicians direct access to alteration of a sound's relative brightness/darkness, and can be used for countless practical and special effects. Subtractive synthesis is perhaps the most common synthesis method to this day—despite its simplicity, it offers a wealth of sonic potential that musicians have enjoyed for decades.
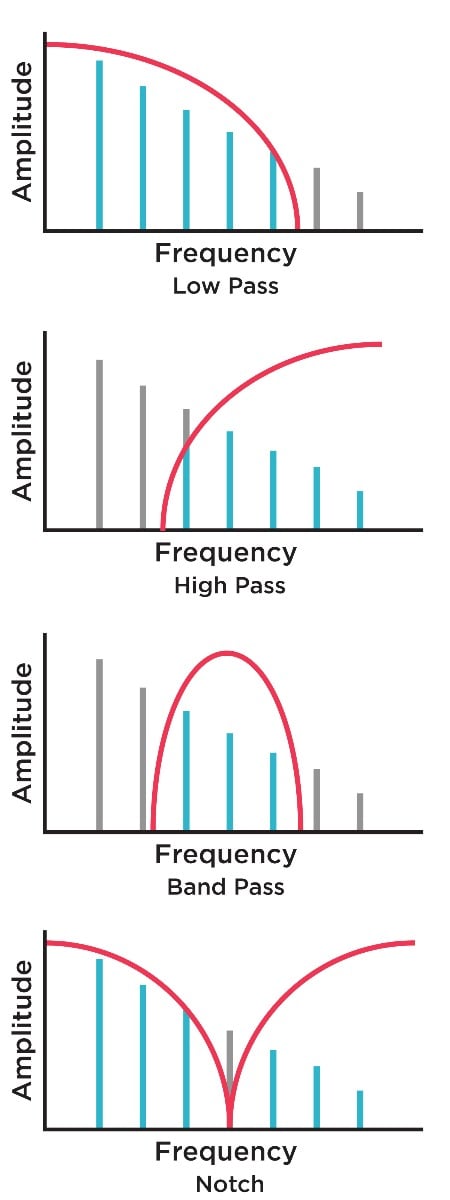Simple spectral view of the four basic filter types, with the passed bands in aqua and the rejected bands in gray.
Who Shall Pass?
There are, of course, many types of filters—but the most common from the 1960s onward are highpass and lowpass filters. Highpass filters remove material low in the audio spectrum, while allowing higher frequencies to pass; lowpass filters do the opposite, removing high frequencies while allowing lower frequencies to pass.
Most filters offer a variable control called cutoff, or cutoff frequency. This is the specific frequency at which the filter begins to take effect. So, for a lowpass filter, all frequencies below the cutoff are allowed to pass; for a highpass filter, all frequencies above the cutoff are allowed to pass. Often, the cutoff frequency is variable: by altering the cutoff in performance, musicians can create brass-like swells, "wow" effects, sounds that seem to disappear into a high fizz, and much more. Because of how powerfully this parameter can affect a sound's character, it is common for the master "cutoff" knob to be one of the most prominent on a synthesizer, with plenty of space around it so that musicians have a visual cue for where to reach in performance.
The next-most-common filter type is the bandpass filter. Bandpass filters allow specific ranges of frequencies to pass, cutting off everything higher and lower than the specified range. For most bandpass filters, the range of frequencies allowed to pass has a fixed width. Some bandpass filters, however, provide an additional control for bandwidth—a variable control for the upper and lower cutoff boundaries, that allows synthesists to hone in on smaller or larger frequency ranges for filtering.
Perhaps the fourth-most-common type of filter is the notch, in which the majority of frequencies pass, except for a small portion which is cut out. Usually this type of filter is reserved for utilitarian purposes, in order to cut out specific unwanted frequencies, but it can also be used to interesting effect, especially when the cutoff frequency is varied during use.
Other Important Terms
Some filters cut virtually all material beyond their cutoff range, while others gradually taper the loudness of the "out of bounds" material for a more gentle and conventionally "musical" sound. Filters with a very sudden, dramatic cutoff are generally referred to as shelving filters, and can often be found in EQs and DJ equipment.
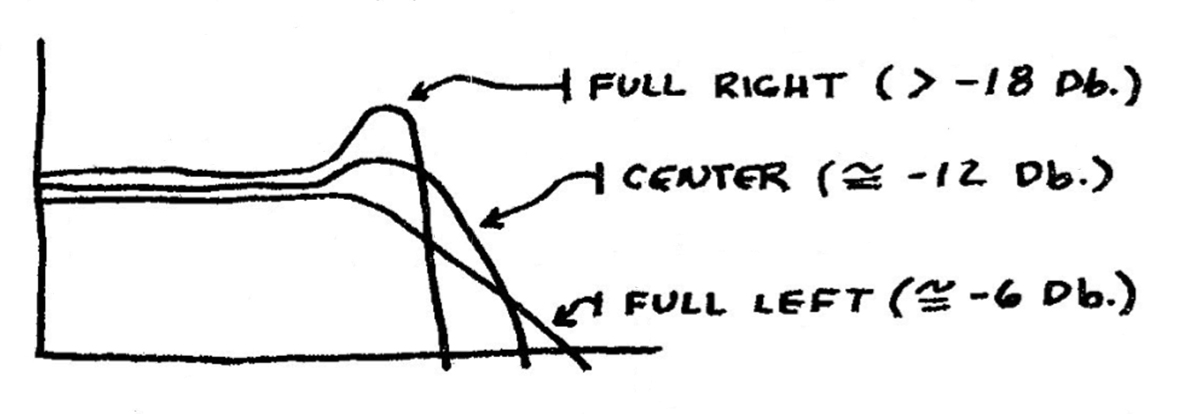Filter slope diagram from a description of the VCFS in a vintage Serge catalog.
The latter category, though, is far more common in synthesizer designs: generally, it is more "smooth" and musically desirable to gradually taper out harmonic material rather than imposing a strict limit on what frequency ranges are heard and not heard. The intensity with which a filter "rolls off" frequencies beyond its cutoff frequency is called slope, and is usually measured in decibels per octave. The most traditional slopes are 12dB/Oct and 24dB/Oct, though other slopes are possible: filters with 6dB/Oct, 18dB/Oct, 36dB/Oct, and 48dB/Oct are less common, but certainly part of the paradigm. Generally speaking, the steepness of the slope relates directly to the intensity of the filtering effect, with 6dB/Oct filters being gentle and soft, and 24dB/Oct filters being comparatively dramatic. Some filters even offer continuously variable slope (such as the Serge VCFS), though these filters are far less common than fixed-slope designs.
Filters also often offer control of resonance, which may also be referred to as Q, Emphasis, or a number of other names depending on the synthesizer. Resonance provides an emphasis to the cutoff frequency itself, often resulting in the filter having a more "wet" sound. For many synthesizers, the resonance is a fixed setting: for more advanced instruments, the resonance itself may be a modulate-able parameter. Altering resonance can have a very different effect from filter to filter, sometimes simply emphasizing overtones near the cutoff frequency, sometimes shifting the sound into more nasal territory, sometimes adding snarl and grit, sometimes pushing the filter into territory not unlike the sound of a physical resonating body.
Many filters are designed in such a way that high resonance settings result in subtle or extreme self-oscillation—that is to say, the filter itself can be made to produce a constant tone simply by virtue of its resonance being set relatively high. In these cases, the pitch of the tone can be altered simply by changing the filter cutoff frequency.
AJH's Minimoog oscillator and Transistor Ladder Filter, complete with self-oscillation and keyboard tracking.
In many keyboard synthesizers, filters offer an option for keyboard tracking: this is, in essence, the ability to link the cutoff frequency in part to the keyboard pitch itself, allowing the filter to open more for higher notes and less for low notes. In many keyboards and synthesizer modules, the filter itself can even track 1V/Oct, making it possible to use the filter as a melodic oscillator when pushed to self-oscillation.
Oh, it's also worth noting that many filters can provide multiple different filter types: so a single filter might offer options to switch between highpass, lowpass, and bandpass modes—or it may even offer simultaneous access to all of these filter types! Filters that offer multiple responses are usually called state-variable filters (SVFs) or multimode filters.
Common uses
One of the simplest and most common "filter-centric" patches involves a single oscillator fed into a filter, which then finds its way to a speaker. Even just by varying the filter's cutoff and resonance, a wealth of different tones may emerge. Commonly, the filter's cutoff is controlled by an envelope, allowing automation of the cutoff over time for a variety of articulations. This is much like the voice architecture in the TB-303, which uses one oscillator and a lowpass filter with an envelope generator that can affect both the cutoff and the resonance (the famous "accent" effect).
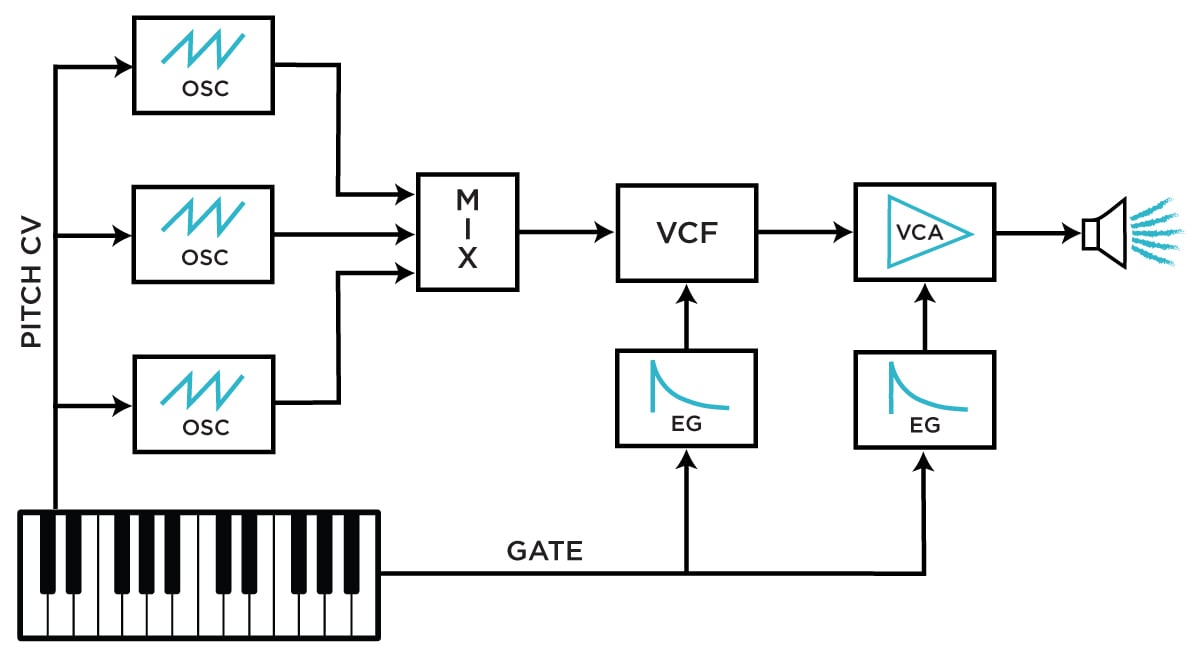
In a typical subtractive keyboard synthesizer, one or several oscillators are mixed together and then fed into a filter (as in the diagram above). The filter's output is fed into a Voltage-Controlled Amplifier (VCA) for dynamic control. The oscillators' pitches are controlled via the keyboard pitch voltage output, and the keyboard's gate output feeds two envelope generators (often ADSR envelopes) which are themselves connected to the modulation inputs for the filter cutoff frequency and VCA gain. This patch is very dynamic, and is the basis for countless keyboard synthesizers—see Moog's Minimoog Model D, ARP's 2600, ARP's Odyssey, and more.
In this patch, variation can occur in a handful of places, but one of the most prominent points of interest is the filter: by altering the cutoff frequency and resonance, the character of the sound can change very quickly. And moreover, by changing the shape and intensity of the envelope applied to the filter, the sound's evolution over time can change dramatically: it could be a quick, forceful thump or a tone that slowly blooms over time. By enabling separately shape-able modulation of the filter's cutoff and the sound's overall dynamic level (via the VCA), this patch provides countless potential relationships between the sound's loudness and timbre. This creates a nearly endless world of potential articulations, and as such has remained a staple default signal path in keyboard subtractive synthesizer design.
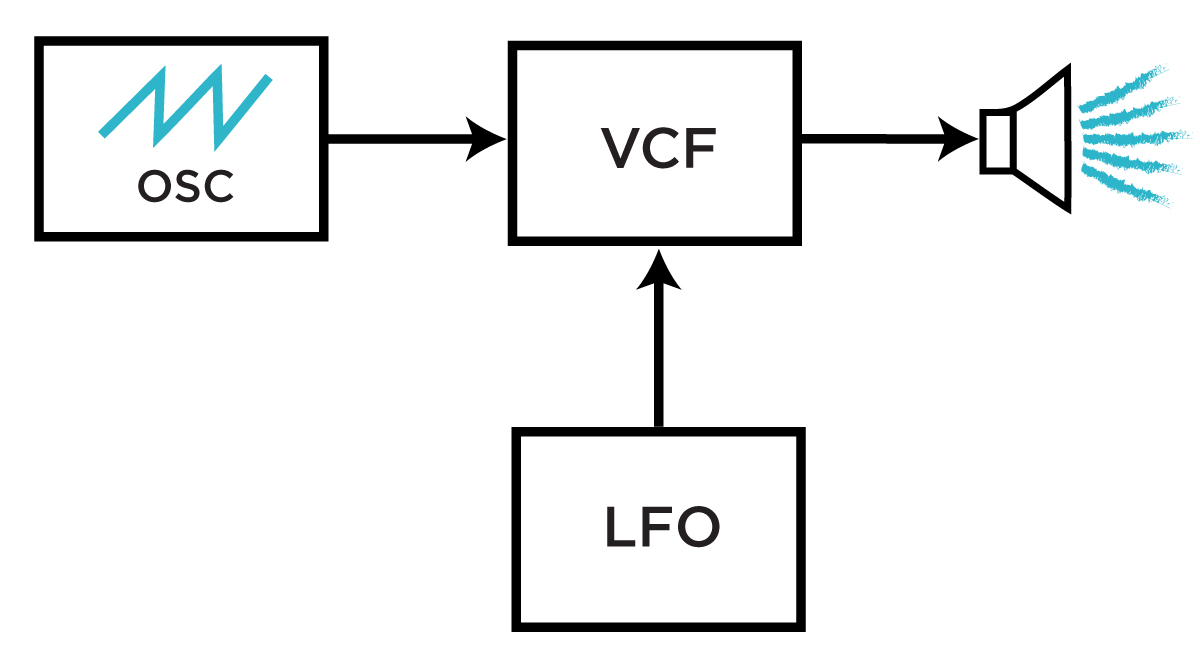Modulating a fitler via LFO.
Another common patch involves using an LFO to modulate a lowpass filter's cutoff. In this scenario, the LFO shape will have a dramatic impact: square wave LFOs will produce sounds that toggle between two different filter cutoff levels, while sine wave LFOs, for instance, will produce a "wobble" effect where the sound's brightness continuously changes. One could replace the LFO in this patch with a Sample & Hold or stepped random voltage source in order to create sudden, jarring changes in brightness: at high resonance settings, this yields a classic sound effect reminiscent of computers in old-school sci-fi films.
Of course, these approaches can also be combined—the possibilities are nearly endless.
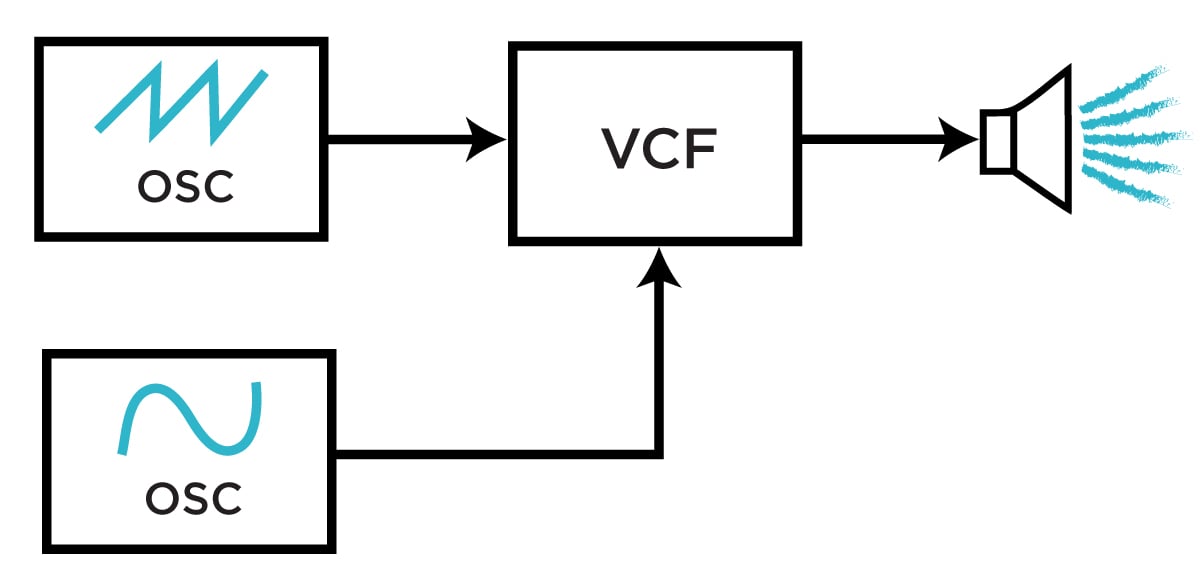A basic, two-oscillator filter FM block diagram.
Odd Uses: Filter FM
There are of course many other things that can be done with filters.
This patch is very similar to the LFO example above...but rather than using an LFO to modulate the filter, a second audio-rate oscillator provides control for the filter's cutoff frequency. This technique is commonly called Filter Frequency Modulation (Filter FM), and is available in countless vintage synthesizers, including the Minimoog and Sequential Circuits Pro One.
This technique can produce sounds similar to traditional frequency modulation. When the two oscillators are tuned to a fairly consonant interval, this results in distortion-like reinforcements of different parts of the sound's natural timbre. When the two oscillators are tuned to relatively dissonant intervals, this results in ring modulation-like inharmonic tones that tear through spacetime.
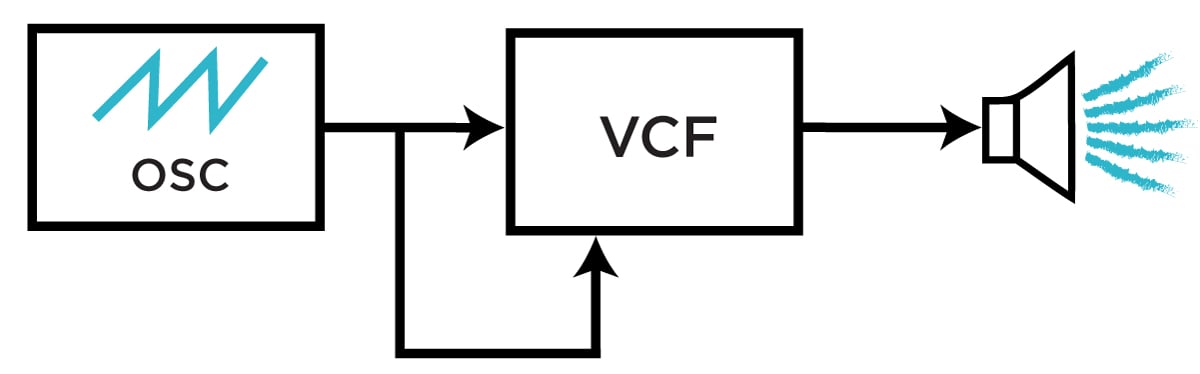A simplified filter FM block diagram using only one oscillator.
This patch can be simplified, as seen to the right: by simultaneously feeding one oscillator to the filter's audio input and cutoff CV input, the distortion-like effects discussed above can be made to track cleanly and consistently without too much inharmonicity coming into play. Try using different waveshapes for the FM signal—even try using a suboscillator for this, if your oscillator has one!
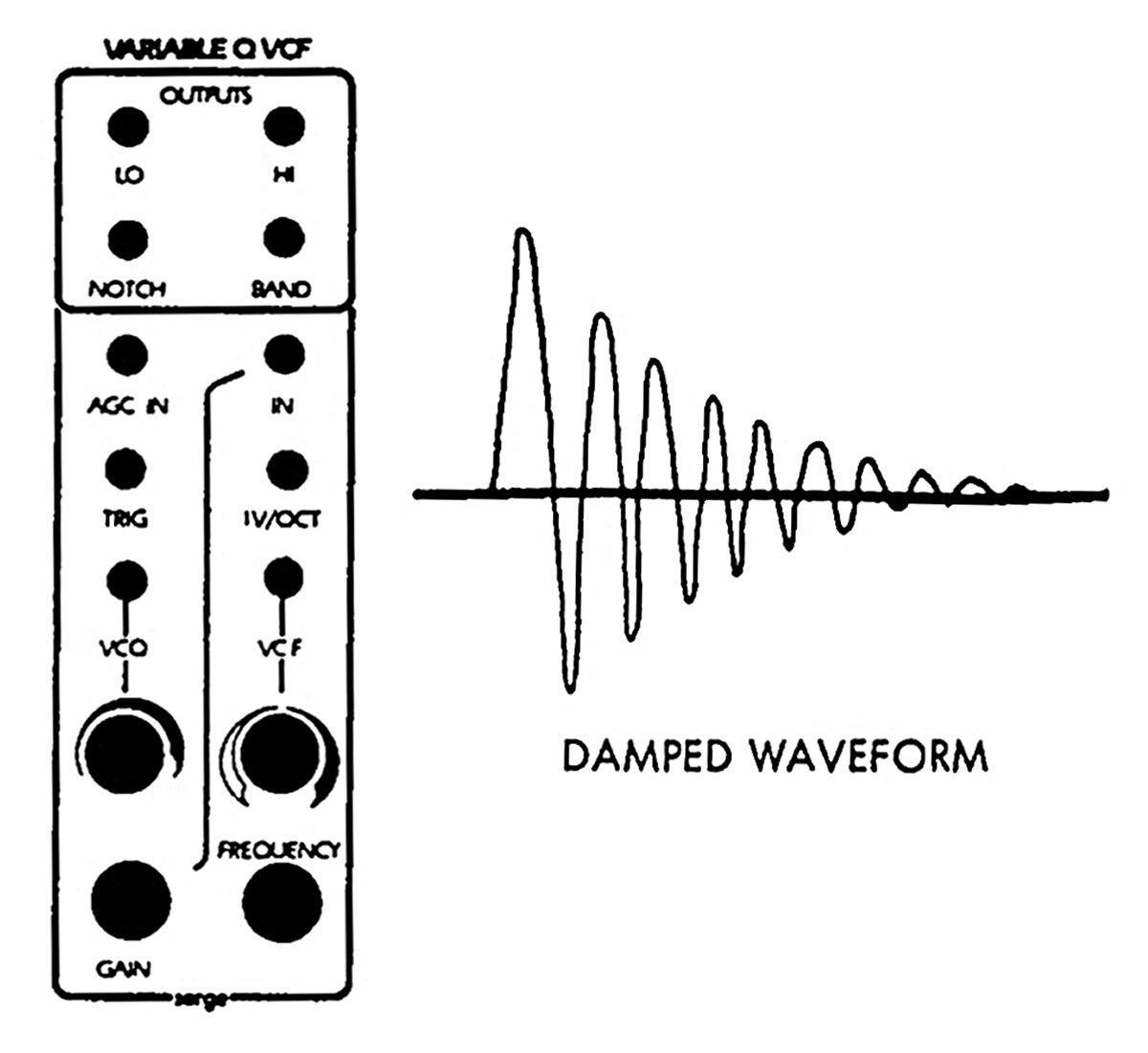VCFQ pinging image from a vintage Serge catalog.
Odd Uses: Pinging!
A handful of oscillators out there have dedicated "ping" inputs. Typically, sending a gate to this input produces a quick, transient pulse that is then processed through the filter. At high resonance settings, this can produce clean, ringing tones much like a decaying sine wave. Some filters designed to exploit this technique include the classic Serge Variable Q VCF (VCFQ, as it is commonly called) and Steady State Fate's MMF.
Many filters will produce similar results if provided transient pulses into their audio inputs, as well! This approach works spectacularly with Make Noise's QPAS, the XAOC Devices Belgrad, and others: just turn the resonance up a good bit, send a pulse in, and listen to the pure ringing tones that emerge. If handled carefully, these sounds can sound strikingly similar to struck clay pots, glass bottles, and more, and can be like entire synth voices unto themselves.
Some Pingable Modular VCFs
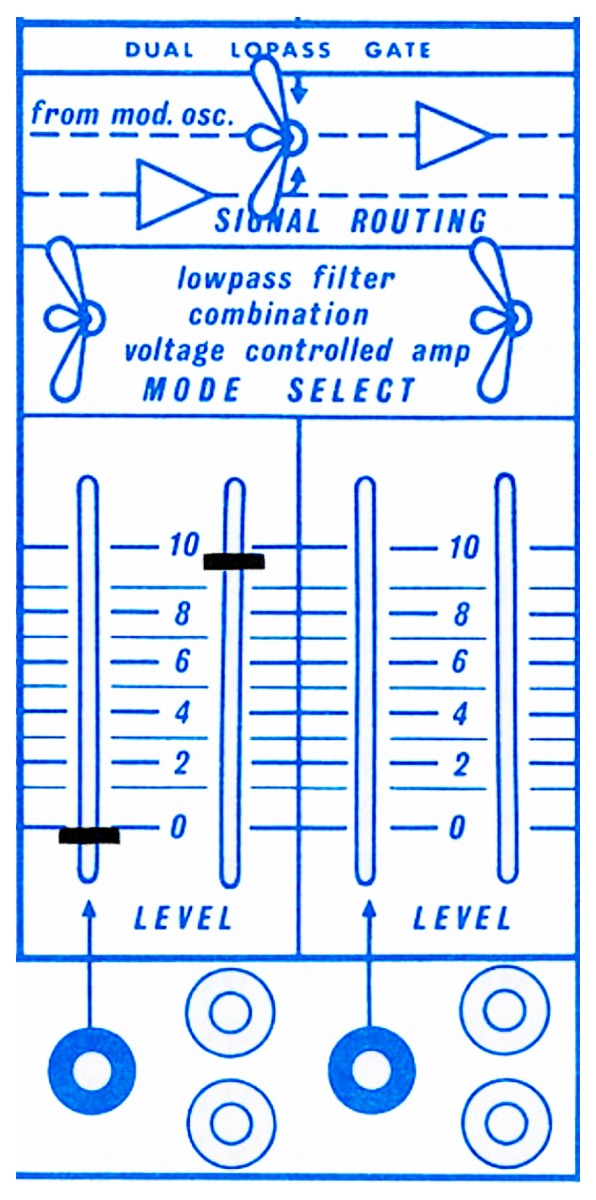Dual Lowpass Gate on Buchla's 208/Music Easel, from Allen Strange's "Programming and Metaprogramming in the Electro Organism."
Other Filter Types: Lowpass Gates
Lowpass gates (LPGs) are a special type of pseudo-filter based on the designs of Don Buchla. Lowpass gates are distinct from typical lowpass filters in that they affect not only a sound's brightness, but also its loudness in tandem. For this reason, they are commonly referred to as lowpass filter-amplifiers. An interesting side effect of this coupling of parameters is that LPGs do quite a good job at creating "organic sounds": sounds that intensify in brightness as they get louder, much like acoustic instruments.
LPGs are most commonly built using a peculiar component called a vactrol. Vactrols are at this point a relatively "outdated" technology based on coupling light-emitting diodes (LEDs) and light-dependent resistors (LDRs, or photoresistors). Because of the LED's naturally slow dimming time, classic LPGs have a relatively sluggish response. This means that they generally won't respond well to the FM tricks outlined above, but the tradeoff is a gentle, plucky/ringing response not unlike a marimba or a small drum (hence the term "Buchla Bongo").
A LPG's slope is generally very gentle (often ~6dB/Oct), and because of their effects on a sound's loudness, they may completely replace filters and/or VCAs in a synthesizer voice. This is the case in Buchla's classic Music Easel, as well as more modern instruments such as the Make Noise Black & Gold Shared System or 0-Coast, Pittsburgh's Microvolt 3900, and Korg's Volca Modular.
LPGs are still relatively uncommon in self-contained synthesizers, but they are now very common in the modular synth realm: some excellent examples include Doepfer's A-101-2 Vactrol Lowpass Gate, Make Noise's Optomix, Malekko Heavy Industry's Richter Dual Borg, Pittsburgh's Dynamic Impulse Filter, and others.
Some Eurorack Lowpass Gates
Other Filter Types: Multi-Peak Filters
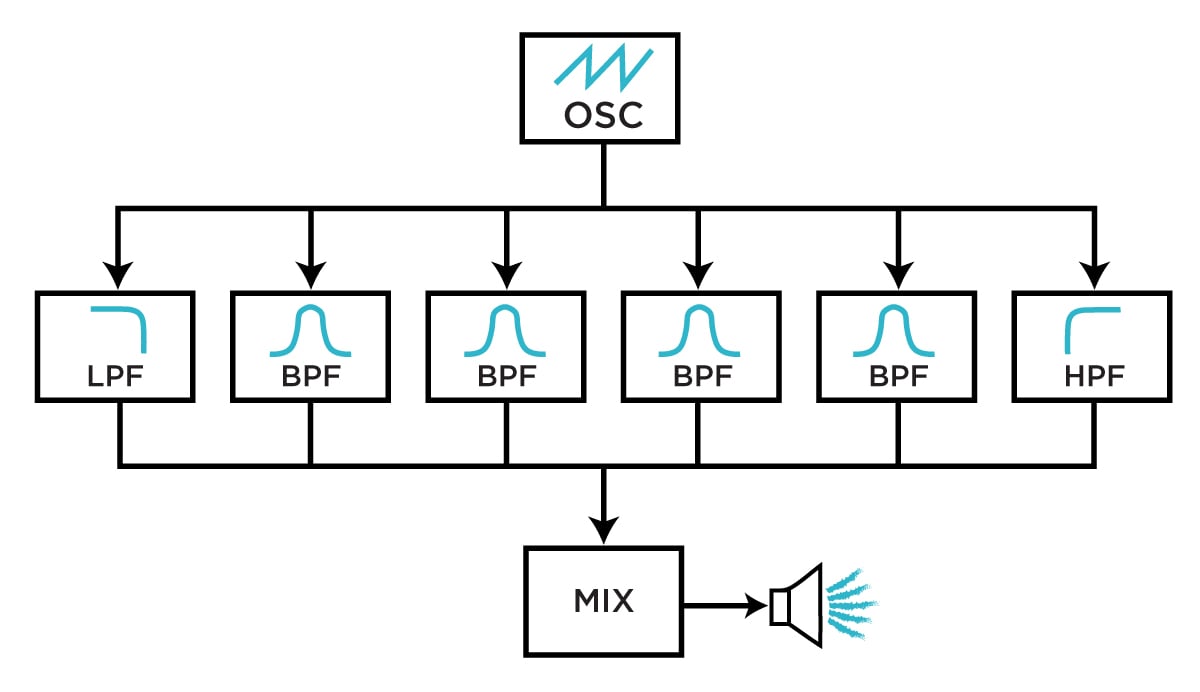
Multi-peak filters combine multiple filters into a single signal path in order to create complex filtering responses not possible with classic filter types. Implementations vary considerably, but most multi-peak filters are comprised of multiple filters in parallel, each fed the same signal and added together to create complex results. The individual filters may be lowpass, bandpass, or highpass types—or perhaps even something more exotic. All peaks offer variable cutoff frequency, often with a single "center" frequency control and a further control for how far the individual peaks stray from the defined center.
Block diagram of a three-core multi-peak filter.
Formant filters fall into this category. Formant filters are typically comprised of multiple bandpass filters in parallel, tuned in such a way that they create a crude approximation of the physical modes of the vocal tract and mouth. It is surprisingly easy to create uncanny vowel sounds with this approach. This technique was famously employed in Synton's Syrinx, a rare keyboard synth from the early 1980s, as well as the Korg PS3100 and Oskar Sala's Mixtur Trautonium—more recently, Modor's NF-1 has employed this technique to peculiar effect.
The XAOC Belgrad and Make Noise QPAS are other noteworthy multi-peak filters. Interestingly, this type of filter seems to commonly be paired with the potential for exploiting the "pinging" technique discussed above. This opens up greater potential for crude physical modeling, and leads to a world of weird sputters, grunts, and gurgles difficult to find through other methods. The Belgrad and QPAS in particular are quite fantastic for this purpose, offering a wide array of novel tone-shaping options.
Other Filter Types: Fixed Filter Banks & EQs
Fixed filter banks (FFBs) are another type of filter uncommon to standalone synthesizers, but relatively common in the modular synth realm. Fixed filter banks are somewhat like graphic equalizers: they are a collection of filters each set to specific frequencies (no variable cutoff frequency here!). Sometimes, each filter will have a direct output available—perhaps more commonly, though, a single mix output is offered, making it such that users can enhance or remove specific spectral regions of a sound. This is not unlike the process of EQing during mixing—but often more dramatic, and for colorful effect rather than simple utilitarian function.
The Moog 907A Fixed Filter Bank.
Like many contemporary synthesis components, these types of filter banks in synthesizers can be traced back to the early designs of Bob Moog and Don Buchla. Bob Moog's early modular instruments included the 907 and 914 Fixed Filter Banks offer low and high shelving filters as well as several relatively steep bandpass filters spaced between. Each band provides a manual level control for easy blending of tones. These filter banks use an inductor-based design, and as such have a unique and spectacular sound. The AJH Fixed Filter Bank 914 is directly inspired by the R. A. Moog 914, and includes some extra niceties not included in the original design. The 907A itself has recently been resurrected as part of Moog's limited series of modular reissues, as seen on the right.
Don Buchla's fixed filter banks evolved substantially throughout the 1960s and 1970s. The 194 Bandpass Filter and 195 Octave Formant Filter were simple designs with input and output jacks, with no built-in mixing capability for the individual bands. This changed in the 200-series revisions of these models, the 294 4-Channel Comb Filter and 295 10-Channel Comb Filter. Perhaps the most remarkable of Buchla's FFB designs, though, is the 296 Programmable Spectral Processor.
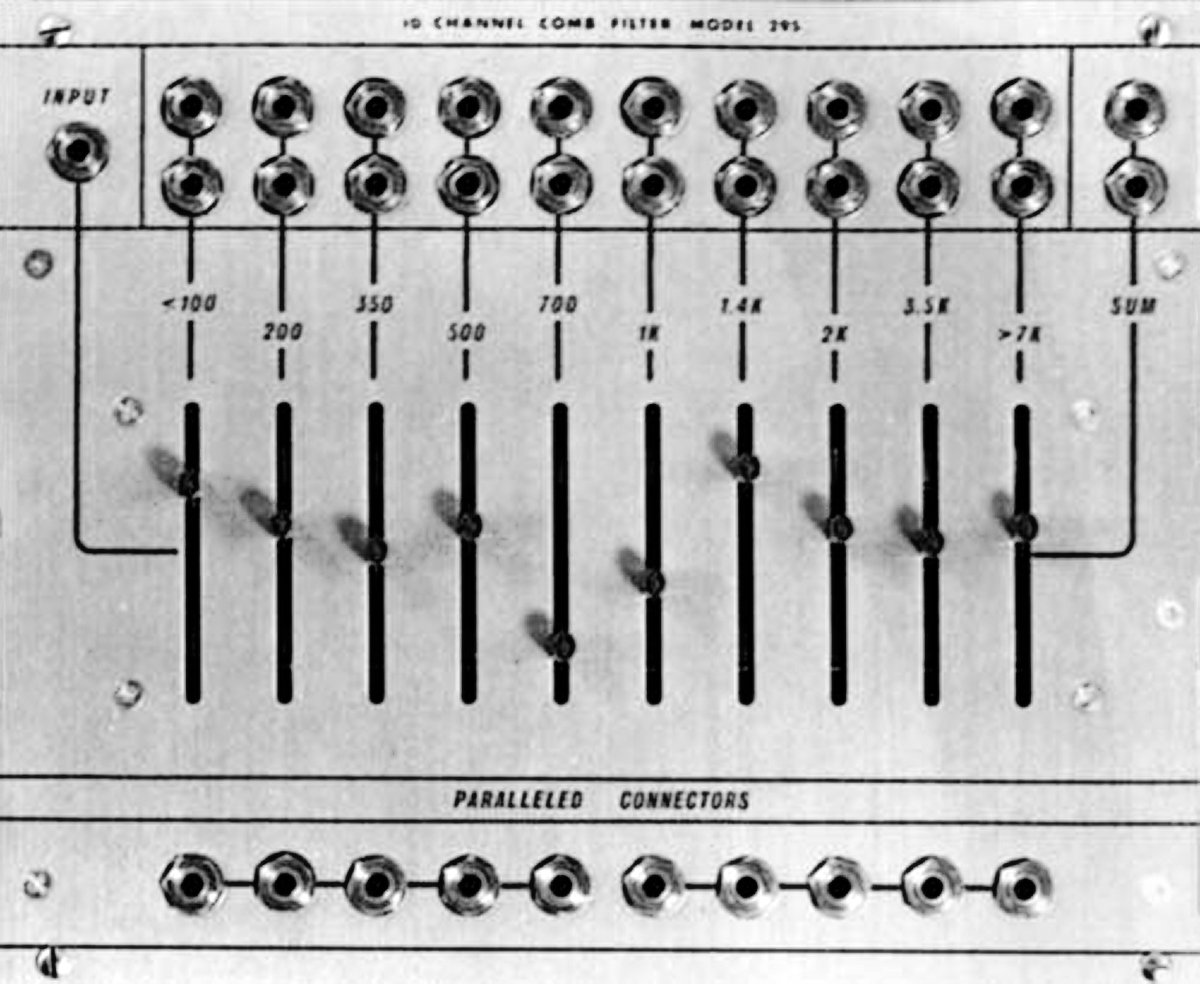The Buchla 295, direct predecessor to the formidable 296 Programmable Spectral Processor.
Buchla's 296 was a 16-band FFB that offered built-in mixing, voltage control of each band's level, a variety of mix outputs, individual outputs for each band, and envelope followers on each band. The integration of envelope followers into the design made it such that the unit could also be used as a vocoder: a means of analyzing the spectral profile of one sound and transferring it onto another sound. Vocoders are their own broad and fascinating topic, which we'll dive deeper into in a future article.
Notable filter banks inspired by the Buchla 296 include the Verbos Bark Filter and Frap Tools Fumana, both fascinating modules that offer their own takes on Buchla's classic design. Other peculiar and imaginative implementations of the broad idea of a FFB can be found in 4ms's SMR, the Random*Source recreation of Serge's Resonant Equalizer, and more. From basic EQing to complex tone shaping, these are uncommonly powerful synthesis resources.
Eurorack-Format Fixed Filterbanks
Other Filter Types: Allpass Filters
Allpass filters are worth a quick mention, although they function very differently from the other types addressed above. Rather than focusing on directly altering a sound's spectral focus, allpass filters introduce very short delay lines and combine them with the dry signal in order to create bizarre phase cancellation effects. And while phase cancellation in the pro audio realm is often an undesirable consequence of poor mic placement, the synthesis realm opens it up as a technique for timbral exploitation.
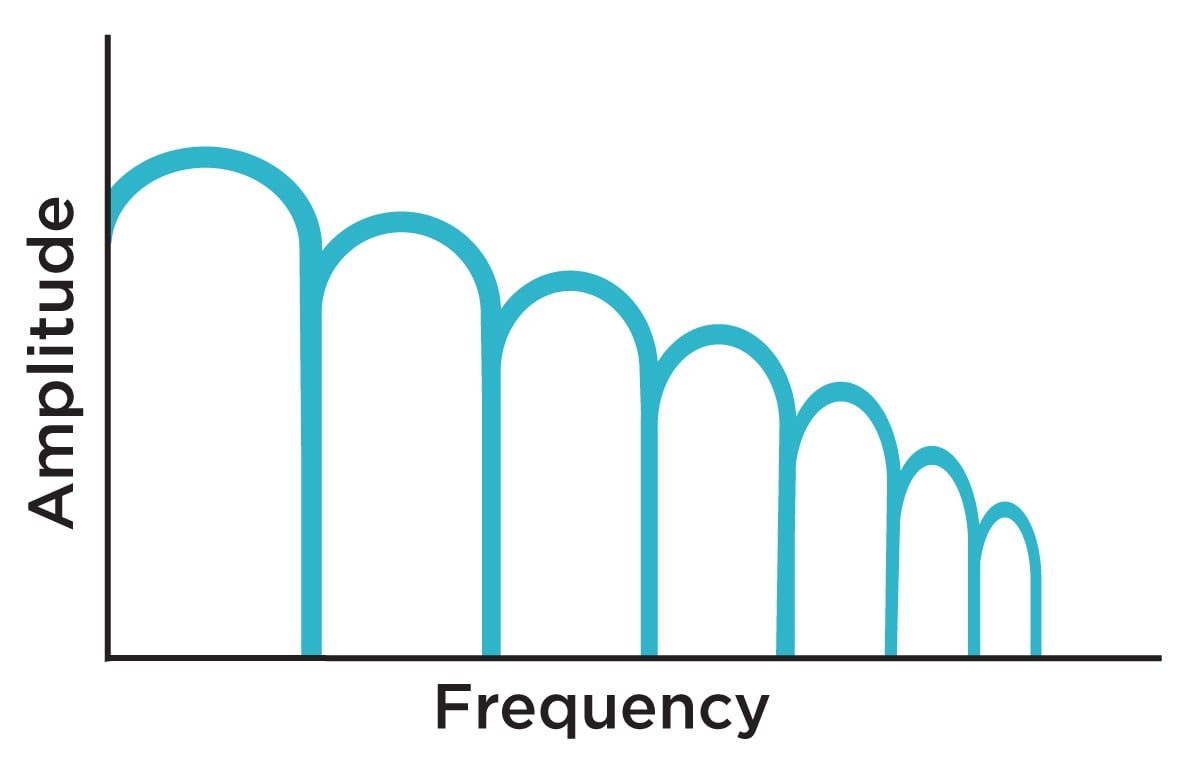A simple diagram illustrating the effects (and namesake) of comb filtering.
Allpass filters can be used as the basis for many effects, from short reverbs to phasers and more. Most often, they are used for comb filtering—a technique provided in Intellijel's Polaris, as well as Modor's NF-1 synth and Comb Filter module. Comb filtering is labelled as such because of the odd spectral effects of phase cancellation: when a sound is mixed together with a very slightly delayed version of itself, the sound develops a series of peaks and troughs in its frequency response that bear resemblance to a comb. When the delay time changes, the position of the comb's teeth in the spectrum change; when modulated with an LFO or envelope, this creates a phaser-type effect.
Allpass filters are far less common than the other types we've discussed, but they can offer very interesting and unique options for sound design.
Vintage Filter Fascination
Analog synthesizer aficionados often treat filters like fine wine: for them, subtle differences in filter designs can make a world of difference in how a patch develops. As such, modern self-contained and modular synthesizers often directly model time-tested vintage filter designs. There are far too many of these topologies to discuss in depth, but it is worth addressing some of the more prominent designs out there.
The Moog 904A—perhaps the most highly regarded lowpass filter of all time.
Perhaps the most famous filter design out there is the transistor ladder filter, a design first implemented in Bob Moog's modular synthesizers. The Moog 904-A is often heralded as the greatest filter of all time, offering a simple set of controls and a steep 24dB/octave slope. This is one of the most iconic filters, with a warm, thumpy sound that defined countless synth basslines. An adaptation of this design was also used in the Minimoog Model D: a primary ingredient in what is perhaps the best-known monosynth of all time. Today, the transistor ladder filter lives on: variants have been used in countless instruments from Arturia's Matrixbrute to Moog's own Grandmother semimodular keyboard synthesizer. In the modular realm, close adaptation can be found in AJH's Minimod VCF, Rossum's Evolution, and Instruo's Traigh.
The EMS VCS3 ("The Putney"), complete with pin matrix, joystick, and diode ladder filter.
Diode ladder filters emerged partly as a way of circumventing Moog's patent on the much-loved transistor ladder design. The diode ladder design was first implemented by EMS in their peculiar line of experimental instruments, including the VCS3 "Putney" and the highly sought-after Synthi A & Synthi AKS. The unpredictable and unstable attributes of this filter lead to an intense, squelchy sound that breaks up in bizarre ways—this response is perhaps best characterized in the Roland TB-303, which used a very similar filter design to create its iconic accents and acidic tones. The Moog Musonics Sonic V, a very rare keyboard synthesizer, also employed a diode ladder design: this filter was recently reincarnated as the Sonic XV by AJH Synth for their line of Moog-inspired Eurorack modules.
A photo of the filter section from Korg's reissued MS-20 mini.
Some of Korg's early keyboard synthesizers offered a peculiar filter design now famous for its aggressive nature and its ability to produce multiple filter responses with ease. Many Korg synthesizers offered two filters per voice: a highpass filter and lowpass filter connected in series, each with separate cutoff controls. This design was first seen in the Korg 770 and Mini-Korg's Traveler filters, but was exposed in full force in their infamous MS-20, a cult favorite due to its intense, aggressive sound. This type of filter is alive and well in such modules as Malekko's Dual Borg, VSL's VCF-74, Befaco's BF-22, and Doepfer's A-106-1 (aptly named the Xtreme Filter).
One of the interesting implications of this approach is that the filter section can seem to morph continuously between different filter types: with the lowpass section fully open, one can generate a simple highpass response by varying the highpass section. Likewise, with the highpass filter all the way down, the lowpass filter is allowed to shine. Everywhere in between, the filter functions as a type of bandpass filter, with the highpass frequency and lowpass frequency acting as the boundaries of the overall bandwidth. The downside to this approach, of course, is that no sound passes if the highpass frequency is higher than the lowpass frequency—effectively rendering the synthesizer mute.
Another famously unstable and colorful filter can be found in the Formanta Polivoks, a Soviet-era synthesizer known for its peculiar take on the standard subtractive analog synthesizer paradigm. The Polivoks filter provides switchable lowpass and bandpass outputs, with a particularly noisy, nasal, and decidedly mean character with resonance added. The bandpass output in particular has a very distinct fizziness, perfect for all manner of electric zapping sounds and screeching resonant sweeps. The Polivoks VCF can be found in several products made by Elta Music, and has also earned dedicated Eurorack recreations by companies such as Industrial Music Electronics (FKA The Harvestman) and Erica Synths. Erica's Acidbox is a desktop filter unit based on the snarly sound of the Polivoks VCF, while Elta's Polivoks Mini is a reduced reimagining of the Polivoks itself.
Manhattan Analog Analog Steiner Synthasystem VCF 14hp- Sale
$219.00 $174.00In Stock Available immediately!
The Steiner-Parker state-variable filter was designed by Nyle Steiner for the Synthacon, a now quite rare monophonic keyboard synth. The Steiner filter is a 12dB/octave SVF, providing lowpass, highpass, and bandpass responses. This filter was largely overlooked until recent years, when its inclusion in Arturia's Minibrute, Microbrute, and Matrixbrute synthesizers brought it back into the limelight.
The Steiner filter has a very special sound at high resonance: while many filters (such as the Minimoog's) suffer a dramatic loss of low-end energy as resonance is increased, the special design of the Steiner filter keeps the level relatively balanced even at high resonance settings. Aside from Arturia's wide use of this design, the Steiner filter can be found in Manhattan Analog's Synthasystem VCF and Tiptop Audio's Forbidden Planet.
Image from the rear cover of the EDP Wasp's user manual.
Honorable mention: Electronic Dream Plant's Wasp synthesizer sported a state-variable filter with lowpass, bandpass, and highpass outputs. This bizarre touch keyboard-based synthesizer is a rarity, but has nonetheless inspired many with its outrageous filter sound. Definitely more on the side of the Polivoks or Synthi than the smooth response of the Moog ladder filter, the Wasp filter is an absolute peculiarity perfect for extremely resonant, aggressive sounds. Doepfer's A-124 VCF5 is a lovely recreation of this famously raunchy filter design.
There are, of course, a million other amazing filters out there—the Curtis filter found in many Sequential Circuits and Dave Smith synthesizers, the beloved SEM filter, countless revisions of ARP filters, Buchla's variable-width bandpass filters, and more. Each one offers its own character and its own shortcomings. And while the obsessive nature of some synth enthusiasts may at first seem unwarranted, even a subtle difference in response can lead to big changes in the end product, whether by some undefinable "magic" or simply by the nature of inspiring the ear of the beholder.
Filters are, no doubt, one of the most loved and most discussed components of any synthesizer: many synthesizers' identity as a whole hinges largely around the sound and response of its internal filtering options. And while not every synthesis method has a solid place for filters, subtractive synthesis is still by far the most common approach—an approach that at its core requires flexible options for tonal shaping.
However, despite their inherently subtractive nature, hopefully this article has also shed some light on how filters can break past their typical role in the subtractive signal path. Filters can drive banks of envelope followers, or they can produce glass-like resonances, or they can turn low-frequency impulses into throat-like gurgles. They are one among the countless tools available to synthesists, which may be used for traditional applications or misused for techniques yet to be discovered.
