Additive synthesis is an often mystifying and somewhat misunderstood sibling of its popular sibling, subtractive synthesis. Subtractive synthesis has unarguably become the prevailing synthesizer architecture since the early days of analog synthesizers. As a result, it has shaped the cultural understanding of what synthesizers are, and how one uses them to create new sounds.

The relative rarity of additive synthesis, however, is not the result of some inferiority—quite the opposite, in fact. The additive method, as some may believe, may be where the future of sound synthesis lies. Through clever implementations, it could technically be employed to facilitate the creation of any sound, acoustic or electronic.

This power, however, comes at a cost. Additive synthesis can get quite complex, and it can be tedious to work with. That said, when approached the right way by instrument designers, the outcome can be quite intuitive and instantaneous. In the course of this article, we will share some ideas regarding why the intricacies of the method can now be managed better than ever before. We will also discuss the general principles of additive synthesis, and explore several historical and modern instruments that incorporate it in their designs.

What is Additive Synthesis?

Before we get into the discussion regarding what additive synthesis is, let's first make it clear what it is not. The drift of popular misconception regarding the so-called "coastal" synthesis dichotomy often carries an idea that the core difference between the approaches of Robert Moog and Don Buchla is that while the former's inventions were driven by the subtractive approach, Buchla synthesizers are additive. This is not the case, strictly speaking. Known for the introducing the concept of wavefolding in instrument design, Buchla instruments are undoubtedly capable of creating complex harmonic tones by processing simple sine waves, but this is not truly additive synthesis—and it may be better understood through the prism of audio waveshaping and distortion techniques.

Period portrait of Joseph Fourier

×

In order to understand how true additive synthesis works, it is important to touch upon one of the most important discoveries about the nature of sound. Thoroughly formulated by the 18th–19th century French mathematician and physicist Joseph Fourier, the Fourier Theorem suggests (among other things) that any sound can be decomposed into a series of individual sine waves. We call these sinusoidal components partials. To further clarify, the word partial is related to the common musical term harmonics, albeit partials can exist above and below the fundamental, and can be harmonically related to it or not. Therefore, partials are more useful for describing sounds indiscriminately, not being merely bound to musical tones with a defined pitch.

In essence, additive synthesis works in reverse of this concept. In additive synthesis, you can create any sound by layering multiple sine waves on top of one another. The volume, phase, and frequency of each partial plays a defining role in establishing the timbre of the tone. Moreover, the quantity of partials has an unequivocal effect on the complexity of the sound: the more sine waves are involved, the more complex the tone can be. Thus, loosely compared to the visual world of pixels, the number of partials corresponds to the resolution of the sound wave.

×

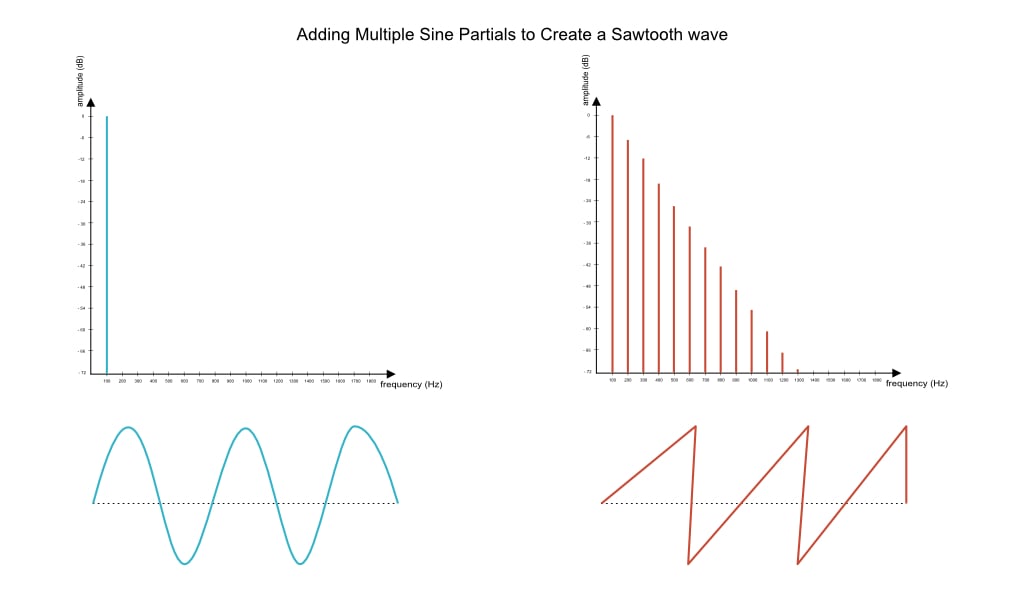
Let's test this by trying to recreate one of the elemental waveshapes using this method—the sawtooth wave. We know that a sawtooth contains both even and odd harmonics (integer multiples of the fundamental frequency). This means that a saw wave at a frequency of 100Hz features harmonics at 200Hz, 300Hz, 400Hz, 500Hz, etc. We also know that the amplitude of each harmonic partial is equal to 1/n, where 1 indicates the maximum amplitude (the loudest partial here is the fundamental), and n stands for the actual sequential number of the partial being calculated. Thus in our example, the amplitude of the second partial will be half the amplitude of the fundamental (1/2), the third partial is one third the maximum amplitude, the fourth is a quarter of the maximum amplitude, and so forth.

For additive synthesis to become practical, a new kind of technology had to be invented, and it was brought by the digital era. With the advent of digital signal processing, it became possible to store and control masses of oscillators in a much smaller form factor, and soon enough some synthesizer manufacturers started to reinvestigate the additive method. But before we look at some of the iconic additive instruments of the last four decades, let's discuss the origins of the additive concept. It turns out that even though Fourier's theory is crucial for the formation of additive synthesizers, on a practical level the method itself has actually been around for centuries.

The Origins of Additive Synthesis

The bona fide archetype of an additive synthesizer is the pipe organ, a massive acoustic instrument that has been around since the 3rd century BC (that in itself is inspired by ancient pan flutes...funny how things work). Of course, there is a lot that differentiates a modern additive synthesizer from an organ, but they overlap in how the timbres of the instruments are shaped. In organs, each pipe produces a single pitch defined by its size and width. Multiple pipes are grouped together into ranks that specify the tone of the instrument, and similarly to a synthesizer, the decision regarding which pipes are combined is left to the performer who manipulates the timbre of the instrument via a collection of hand stops and combination pistons.

×

The scientist and philosopher Hermann von Helmholtz was particularly interested in all things related to human visual and auditory perception, and as such, he devised a number of tools to aid in his investigations. Among those tools was what could be said to be an electro-mechanical additive synthesizer known as the Helmholtz Sound Synthesizer (~1862—pictured above, image via Harvard University). The instrument featured an array of electrically-excitable tuning forks. The sounds of multiple tuning forks were combined to generate new timbres. This, of course, was not a tool for creating music, but an experimental instrument for studying sound.

The first electronic instrument based on the additive approach was the legendary Telharmonium, created by Thadeus Cahill at the dusk of the 19th century. Essentially, Telharmonium was an organ-inspired synthesizer that did away with windpipes in favor of gears, coils, magnets, wires, and speakers. While Telharmonium was known for being able to produce extremely pure-sounding sine waves, Cahill endowed the instrument with the mechanism for altering its timbre—tonewheels, the same technology that would later be used in the iconic electric organ Hammond B3, although implemented in a much larger scale. Telharmonium was a colossal building-sized instrument. Its enormity and great appetite for electric power among other practical considerations meant that it wasn't operational for long. Regardless, it remains one of the defining inventions in electronic music history, often cited as the first synthesizer. Importantly for the topic of our discussion, it was most likely the first device we might classify as an additive synthesizer, specifically.

Telharmonium and Hammond B3 were not the only additive-style instruments that were created during the first half of the 20th century. Other notable inventions include ANS (1958), an esoteric optical synthesizer by Evgeny Murzin, Hugh Le Caine's Spectrogram (1959), and James Beauchamp's Harmonic Tone Generator (1964). Notably, these inventions were not produced commercially, and were either private or institution-sponsored experimental developments.

As we've indicated earlier it was the rapid advancement of digital technology in the 1970s and '80s that truly marked the possibility of reevaluating the potential of the additive synthesis method, and finally made it viable to implement the technique in a commercial context. Notable instruments that explored the additive synthesis of that era include RMI Harmonic Synthesizer (1974), Fairlight CMI (1979), New England Digital Synclavier II (1979), Kawai K5m (1987), Wersi EX20 (1986), and Technos Acxel (1988)—the CMI, Synclavier, and Acxel are picture above.

It is also worth noting that although we explicitly said at the beginning of this article that Buchla synthesizers do not fall directly into the additive synthesis category, Don did create some modules that promoted this approach. A good example of such is the 148 Harmonic Generator module created in late 1960s as a part of the 100 Series system. A similar design has been revived in the Eurorack format by Verbos Electronics, re-titled as the Harmonic Oscillator. Later Buchla instruments such as the Touché, 400, and 700 explored additive-adjacent techniques through the use of sophisticated waveshaping techniques—but we'll talk about all of that in another article.

An Alternate Approach: Resynthesis

A peculiar and still rather underexplored derivative of additive synthesis is a method of working with sound known as resynthesis. In resynthesis, an existing sound is subjected to a Fourier analysis, and the instrument retunes its internal bank of oscillators to correspond to the extracted data. Once the essence of the "real" sound has been "cloned", various operations can be applied to alter it, including retuning, stretching, compressing, and completely restructuring it. Not all additive synthesizers are capable of resynthesis, and similarly not all the specifically resynthesis-oriented devices offer regular additive synthesis workflows, but there are many overlaps.

The aforementioned Technos Acxel allowed both and was highly optimized for resynthesis. Rossum Electro-Music's Panharmonium brought the power of spectral resynthesis to the domain of Eurorack-format modular synthesizers, and more recently, the Make Noise soundhack Spectraphon has emerged, offering its own curious take on additive synthesis and resynthesis. The iconic software instrument Metasynth also offers a number of options for both ANS-inspired additive synthesis and resynthesis explorations.

Managing Complexity

×

[Above: a visualization of the spectrum of a music box.]

Although the vastly powerful digital tools of the modern age make additive synthesis more approachable than ever before, one of the core challenges of this method remains in finding ways to make additive-style devices feel like instruments. After all, individually tuning giant banks of oscillators, and individually assigning a dynamic profile to each partial can easily turn into a laborious, and even monotonous process—this is certainly not the best-loved aspect of making music for most of us. Therefore, a certain ingenuity is required from the side of the designer-manufacturer to make additive synthesis usable, and enjoyable to work with, and this results in great variance in the instruments of this category.

For example, the Metasynth software mentioned in the previous section offers its users a digital canvas for painting musical ideas...literally. Shapes, positions, and colors are read by the software and reinterpreted as sound parameters. Native Instrument's outstanding Razor synthesizer camouflages the additive nature of the instrument with a familiar subtractive-like visual separation between the instrument's modules. The nucleus of the instrument is a single massive oscillator bank comprising up to 320 partials, which is segmented into several modules named filters, oscillators, and effects. And although the functions of these modules do somewhat correspond to their names, in actuality each of them performs operations on the groups of partials such as stretching, condensing, attenuating, and moving them around.

Additive synthesis is now also available, and importantly easily manageable in the analog modular format. Besides the earlier mentioned resynthesis toosl Panharmonium and Spectraphon, as well as the Verbos Harmonic Oscillator, several other companies have also started to create advanced instruments for additive synthesis. Great examples include the remarkable additive oscillators Odessa from XAOC Devices (video embedded above) and Ensemble Oscillator by 4MS, each of which offer a macro-style parameterization to minimize the number of user controls for defining timbre. This is in some ways a compromise relative to having per-partial controls...but it's a significant practical consideration that make it possible to intuitively explore a huge range of sounds that othewise wouldn't be possible. Simply put, they're awesome.

Pros and Cons

Perhaps both the strengths and the weaknesses of additive synthesis lie in its complexity. The method offers immense potential for realizing even the most intricate, and nuanced sonic ideas, yet it is certainly not light on resources, and without a well-thought-out and well-optimized system for creative use, it can easily become daunting.

Happily, the modern world of synthesizer development has no shortage of great minds, and as of now, there are already a number of sophisticated and highly-rewarding additive-style instruments to explore. And with the ever-increasing processing power of digital tools, deep learning, and artificial intelligence tools, we can only imagine what is yet to come.