It's not unlike Make Noise to take an entirely unexpected direction in electronic instrument design. While others are out designing spec-sheet-derived filters, analog oscillators, and ADSR envelopes, Make Noise looks to more obscure, un-mined places for inspiration, and they always have. Take the game-changing DPO, for instance: the current Eurorack landscape is full of Buchla 259-derived analog complex oscillators, but DPO was one of the first. Think of Phonogene, one of the first commercially-available implementations of granular synthesis, or the 0-Coast semi-modular desktop synthesizer, or their many collaborative designs with Tom Erbe of SoundHack, or their unrelenting embrace of stereo sound generation and manipulation. My point is this: Make Noise's instruments dive deep into untapped wells of synthesis and sound manipulation, into techniques previously unexplored in modular synthesizers...and often, they've proven to set the tone and standards of Eurorack design as a whole.
Today, Make Noise announces perhaps their most ambitious device to date: the SoundHack Spectraphon. Spectraphon is a digital oscillator arranged more or less like a typical "complex oscillator," somewhat like their all-analog DPO; however, to think of Spectraphon as simply "another complex oscillator" wouldn't be entirely accurate. Rather than focusing on waveshaping as the key to generating complex timbres, Spectraphon instead uses a clever implementation of additive synthesis and re-synthesis-like approaches to turn any sound into a timbral profile for its two oscillators. Spectraphon can generate sound based on stored analyses of external sound sources—or it can even re-synthesize external audio in real time. You can think of this in a number of ways: it can behave somewhat like a vocoder, or it can behave somewhat like a resonator. Similarly, you could think of it as an oscillator whose timbre is "driven" in real time by external sounds—or, you could think of it as a way of creating deep, rich, spectrally-evolving tones from any sound that you encounter. In fact, the nature of some of Spectraphon's controls make it such that you can treat it more or less like two full synth voices, minus envelopes.
In the years following their formation, Make Noise developed a reputation for producing Buchla-like designs. This is fair enough—their DPO, QMMG, Maths, Optomix, and other modules certainly look to Don Buchla's 1970s designs as a source of inspiration. At the same time, though, they were developing advanced digital processing modules, such as the Echophon, Erbe-Verb, Morphagene, and others. And of course, in recent years, we've seen them turn to a focus on digital sound generation and manipulation, as evidenced in the Mimeophon Stereo Color Audio Repeater, the XPO Stereo Prismatic Oscillator, and other designs. I see Spectraphon as a convergence of all of these design directions: it borrows inspiration from several rare/obscure Buchla designs, but takes a starkly different, digital approach to sound generation. Simultaneously, it's quite capable of stereo/multi-channel audio generation and processing, should you choose to patch it that way. It's lovely when a plan comes together, eh?
Okay. So, explaining what Spectraphon is and how it works is a bit of an endeavor, as I'm sure you can tell—so, in this article, I'm going to break it down in several stages. First, I'm going to talk about some of the inspiration behind Spectraphon, as well as the technological developments that made it possible. Afterward, I'll dive into a deeper exploration of how Spectraphon works, including more detailed explanations of its Spectral Amplitude Modulation and Spectral Array Oscillation modes, and how they each uniquely tackle aspects of additive synthesis and resynthesis.
So, let's dive in.
Spectraphon: Inspiration
Spectraphon is, as stated above, a digital oscillator arranged somewhat like a typical "complex oscillator," designed to provide access to continually-evolving, constantly-shifting timbres in several sonic dimensions. Make Noise points to several vintage Buchla designs as being directly inspirational to the Spectraphon's design: the 259 Programmable Complex Waveform Generator, the 296 Programmable Spectral Processor, and the Touché, a hybrid digital/analog keyboard instrument. Interestingly, each of these devices also present their own unique takes on how to generate/manipulate sounds in a continuous fashion. Let's examine the key points about each of these devices to gain a better understanding of how they might have influenced Spectraphon's design. In the end, it'll make understanding Spectraphon a bit simpler.
The most obvious inspiration for Spectraphon lies in the 259, of course. Don Buchla's 259 Programmable Complex Waveform Generator is a rare module developed for Buchla's later 200 and 300 Series modular systems, and it has become something of a cult icon among modular synthesizer enthusiasts: in fact, it's the exact place where the modern concept of a "complex oscillator" fully solidified (though of course, it was not the first Buchla design that implemented a "complex oscillator"). To understand what makes the 259 special, it's first important to consider what most other oscillator designs in the 1970s were like. Many offered only fixed waveshape outputs; so, a single oscillator could produce, for example, a triangle wave, or a saw wave, or a pulse wave...occasionally with the choice to mix multiple shapes together. Instead, more complex tones were typically generated by mixing multiple oscillators together, or by using a filter to carve out or emphasize specific parts of a sound's spectrum.

[Above: an original Buchla 259, part of the 200 system housed at the University of Victoria, BC, Canada.]
The 259 took a quite different approach. First things first, the 259 contains two oscillators: a "Modulation Oscillator" on the left, and a "Principal Oscillator" on the right. The 259 includes a network of internal connections that allow the Modulation oscillator to affect the Principal oscillator in a variety of ways without the need to use patch cables. Using controls in the center of the panel, the Modulation oscillator can be set to modulate the Principal oscillator's amplitude, its frequency, or its timbre. These modulation types can be combined at will, and the modulation depth/intensity can be controlled via a dedicated "modulation index" control—which itself is voltage-controllable. The modulation oscillator offers front-panel access to triangle, saw, or square shapes, and can operate in low or high frequency ranges. Of course, internal provisions for dynamic/variable-depth amplitude and frequency modulation can already create a wide variety of continuously-variable timbres...but the 259's biggest claim to fame is about more than that.

On the right-hand side of the module, you'll notice a section labeled "Harmonics" and a section labeled "Timbre." These controls work in tandem with one another to define the timbre at the Principal oscillator's "Final" output. The Timbre control is perhaps the most iconic and influential: it is a control for the gain of the oscillator's sine signal prior to a peculiar circuit now commonly referred to as a "wavefolder." The net effect of this control is quite striking: fully counterclockwise, the Final output produces a sine-like shape, but as you increase the Timbre control, the sine wave begins to fold over onto itself at its upper and lower boundaries—creating a cascading, constantly evolving, spiraling set of overtones that get gradually brighter and more nasal as it goes along. The Symmetry and Order controls alter the emphasis on Odd vs. Even partials, and Low vs. High partials, respectively, allowing you to introduce a more saw or square-like buzz into the already quite complex final output, and altering the emphasis the Timbre control has on different parts of the sound's harmonic spectrum.
The 259 is quite striking, but the point here is this: it provided many ways to continuously vary the timbre of its sound. It doesn't just give you a few waveshapes you can switch or blend between: it has several controls that allow you to access an astonishing range of timbres. It's easy to get lost listening to even the most subtle variations of a 259's Mod Index or Timbre controls; each can have a profound impact on the sound's spectrum, and the way it evolves over time.
The 296 Programmable Spectral Processor offers its own methods of manipulating the timbre or spectrum of sound. The 296 is, at its core, a fixed filter bank: a collection of sixteen filters at fixed frequencies (one lowpass, fourteen bandpass, and one highpass), each with multiple ways of controlling its loudness. Looking at the panel, you'll see an astounding number of inputs and outputs; CV inputs and outputs from each filter band, direct audio outputs from each band, and a variety of combined output sections. To better understand how 296 works, looking at its output sections is key.

[Above: an original Buchla 296, part of the 200 system housed at the University of Victoria, BC, Canada.]
First of all, despite its many outputs, the 296 has only three inputs: one which goes to All filters, one which goes only to the Even-numbered filters (0–E), and one which goes only to the Odd-numbered filters (1–F). The three primary output sections make use of the Odd and Even filters in a variety of ways. The Comb Filter Outputs are simplest: they're a fixed sum of all of the Even and Odd filters, respectively. The Attenuator Outputs are simple to understand, as well: they're mixed outputs of the Even, Odd, and All filters, with the level of each determined by the array of front-panel sliders. The Programmed Outputs are a bit more complex, and for our current purposes, of greatest interest: these outputs can respond in a variety of ways to external and internal voltage control. The Program Control section allows you to treat the entire module somewhat like a variable-width bandpass filter: the Frequency and Width controls allow you to "scan" the filterbank and alter the "width" of the scanning window, in a sense. The Programmed Outputs also respect the per-filter CV inputs, for a more direct/discrete method of control.
The Programmed Outputs also make use of the Programmed Spectrum Transfer section. It's worth noting that each filter band has a dedicated envelope follower connected to it—translating the loudness of that specific filter into a control voltage that can be used in any way you might please. The Programmed Spectrum Transfer section is a way of internally connecting the envelope follower outputs from the even filters to the CV inputs of the odd filters, or vice versa. If you think about it, this behavior is somewhat like a crude vocoder: it allows you to apply an analysis of eight filters' loudness onto the perceived loudness of the other eight filters. If you apply different sounds to the Even and Odd filters, transfer the Even spectral information onto the Odd bands, and then monitor only the Odd bands, for instance, you'll be able to apply the spectral profile of the Even sound onto the Odd sound—continuously altering its sonic character in relation to another sound in real time. Spoiler alert—this is very much a key idea in how Spectraphon works; and moreover, the concept of dividing a single sound into "even" and "odd" components will come back later as well.
Finally, Make Noise points to the Buchla Touché as a source of inspiration for Spectraphon's design. The Touché was a hybrid eight-voice polyphonic keyboard synthesizer developed from a collaboration between Don Buchla and performer/composer/educator David Rosenboom. The Touché was revolutionary in its time for a number of reasons—it included a compact computer for handling quite complex arrangements of sound and control-oriented tasks, and incorporated a fairly sophisticated system of digital sound generation.

[Above: the Buchla Touché, as pictured in the original product brochure.]
The Touche featured eight voices, each with three oscillators. We can think of the arrangement of oscillators as being somewhat similar to the 259: there is a Principal oscillator for sound generation, which offers continuously variable Timbre; and there are two modulation oscillators, one which can modulate the Principal oscillator's frequency, the other of which can modulate the Principal oscillator's timbre. While the parameterization might sound similar, the Touché's method of "Timbre" generation is implemented quite differently from on the 259. Rather than passing an oscillator through a network of analog circuitry for "wavefolding," the Touche instead passes a sinusoidal oscillator through a digital representation of a nonlinear shaping structure: a "lookup table" which is constantly scanned, back and forth, by the incoming sine wave. The instantaneous amplitude at the output of the waveshaper is determined by the instantaneous amplitude of the sine wave, and how that maps onto different positions in the table. The Timbre control affects the amplitude of the sine wave prior to the nonlinear lookup table; at lower amplitudes, the sine wave sweeps values toward the center of the table, but as its amplitude is increased, it scans a wider region of the table. The end result is a sort of digital distortion—which, with the right values in the table, can sound astonishingly similar to a wavefolder.
 Tables populated with the first eight Chebyshev polynomials of the first kind
Tables populated with the first eight Chebyshev polynomials of the first kind
The contents of the lookup table constitute a transfer function that has a dramatic impact on the character of the sound. One of the interesting characteristics of this method of waveshaping is that, if the table is populated with a special set of shapes known as Chebyshev polynomials, the net effect is that the output of the waveshaper will be some specific harmonic overtone of the incoming sine wave. For instance, by populating the table with the 13th Chebyshev polynomial of the first kind and then running a full-amplitude sine into the shaper will produce a sine wave with 13 times the frequency of the incoming sine wave. By populating the table with an average of the third, fifth, and seventeenth Chebyshev polynomials of the first kind, the output would be equivalent to the mixture of three sine waves at three, five, and seventeen times the frequency of the incoming sine wave. By continuously varying the amplitude of the incoming sine wave, you could get all manner of sounds that brought more or less focus to these overtones. By modulating the amplitude (Timbre) at audio rates, you could get quite wild sounds.
If all that seems like a ton of confusing math talk, don't worry. There's a point I'm trying to make. This method of waveshaping was all the rage among 1970s/1980s computer music researchers because it provided an insanely efficient means by which to—in a roundabout way—approach an otherwise very complex synthesis method: additive synthesis.
Additive Synthesis is a Headache
True additive synthesis is, well, complex. The basic premise of additive synthesis relies on the findings of 19th-century mathematician/physicist Joseph Fourier. The Fourier Theorem has countless applications in the word of science and mathematics, but in the world of music and sound-making, it has some particularly potent implications. In short, for our purposes, the Fourier Theorem states that any reasonably periodic complex functions may be described as a combination of simpler sinusoidal functions operating at multiples of the total function's period. Okay, I know that's probably sounding awfully math-y again, and I apologize—but with a couple of conceptual leaps, we can say this: the Fourier Theorem implies that any complex musical tone can be approximated by using a series of sine waves tuned to very specific frequencies and amplitudes relative to one another. It's fairly simple, for instance, to use a large number of specifically-tuned sine waves to approximate the shape of a saw wave or square wave, for instance.
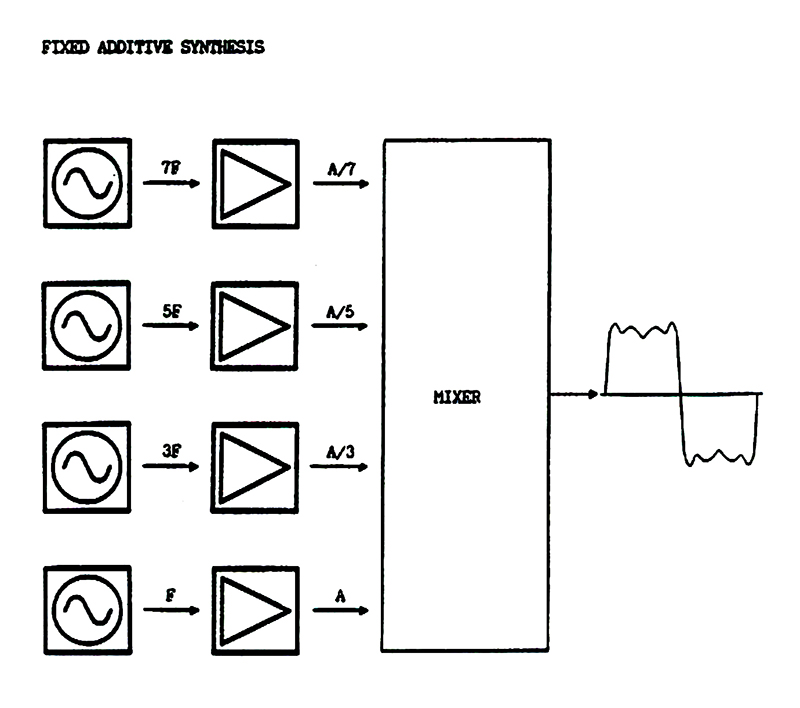
So it's fair to say that if you had enough sine wave oscillators and a big enough mixer, you could construct any periodic timbre. But there are some problems here! 1) How the heck can you precisely and efficiently control dozens (or even hundreds??) of oscillators in a remotely fun way? 2) That's great for creating static timbres...but in the real world, timbres change over time. So, how the heck do you control the way that the tuning and loudness of dozens (or, yep, even hundreds) of oscillators evolves over time? Additive synthesis, while certainly effective and theoretically sound, bears the burden of being an insanely brute-force method of sound shaping. It's just not practical to define frequency relationships, loudness, and envelope shapes for that many sound sources, especially in a hardware-centric design: it's too many controls, each of which ultimately has a relatively subtle effect on the net result.
That's why there have been so few attempts to implement additive synthesis in hardware—synthesizer designers were generally happy enough to explore the potential of subtractive synthesis and other methods of tone-shaping in the early days of synthesizer development. And simultaneously, that's why methods like lookup tables based on Chebyshev polynomials became the focus of much research in the 1970s: it offered an alternative to subtractive synthesis which could provide the option for precisely-constructed timbres without the need to handle insane numbers of oscillators. However, lookup table-based waveshaping wasn't implemented in many hardware designs either (though it remained a focus in Buchla's 400, 700, and 200e instruments). Instead, as computer power and memory increased, it became more economical for instruments to use different approaches altogether: sampling, FM/phase modulation, or other proprietary sound manipulation methods.
Of course, additive synthesis remained a point of interest—as computers became more powerful and instruments adopted more sophisticated computational hardware, suddenly additive synthesis was a viable possibility—just a possibility that still lacked an effective control structure. One of the most promising developments in the 1980s, though, was resynthesis. In most implementations of resynthesis, a specialized process called a Fourier transform (yep, that Fourier) is used to analyze the spectrum of a sound, and ultimately to describe it as a function of many sinusoidal partial tones. By continuously performing Fourier transforms as a sound occurs, it's possible to create a conceptual, multi-dimensional "map" of a sound: you can capture information about which overtones comprise a sound, how loud they are relative to one another, and how the emphasis of different overtones change over time. If you have the ability to store that information as a set of analyses of a sound at different points in time, you suddenly have a list of ingredients for how to re-create the sound using a large number of sine waves. In most situations, that is what resynthesis is all about. (Note: Fourier transforms are not the only way to capture or represent this information—and hypothetically, any method for analyzing a sound's spectrum could be used as the basis for resynthesis.)

Resynthesis has only been implemented in a small handful of hardware designs—again, because it's a relatively complex process which requires a fair amount of computational power, and a lot of careful thought given to what sort of user interface is required. It was part of instruments like the late 1980s/early 1990s Technos Acxel (which I can't help but mention, because it's awesome—pictured above), and has since been implemented in a number of software-based contexts; however, it's still quite uncommon in the realm of hardware. However, it has an insane amount of promise as a control method for additive synthesis: rather than needing a knob or envelope generator for the frequency or loudness of hundreds of oscillators, you can simply analyze a sound that already exists in order to translate it into a series of instructions for that giant bank of oscillators.
And of course, the raw data from the analysis can be used in any number of ways: you can directly re-map it onto a bank of oscillators, or, happily, you can mess with the data—introducing a sonic disconnect between the sound that you analyzed and the sound that you wind up hearing. This, for me, is one of the most interesting aspects of resynthesis...and happily, it's brought directly into focus with Spectraphon. So, now that we have all of that stuff out of the way, let's actually talk about Spectraphon. (And thanks for humoring my perhaps excessive nerdiness.)
Spectraphon Overview
Now that we've gone through so many layers of history and synthesis theory, Spectraphon should be a bit simpler to explain—so let's give it a shot. The Make Noise SoundHack Spectraphon is a dual digital oscillator designed for the creation of complex, continuously evolving sonic spectra. Its layout is quite similar to a Buchla 259—though, unlike the 259, each of Spectraphon's oscillators are more or less identical to one another. Also unlike the 259, it doesn't rely on analog waveshaping in order to create sonic interest: instead, it relies on analysis of external sound sources to perform an abstract version of additive synthesis. (Hopefully, with all that in mind, my long divergence into the Buchla 259, 296, and Touché makes sense?) Spectraphon's two oscillators can each work in one of two modes: Spectral Amplitude Modulation (SAM) in which it analyzes and resynthesizes incoming audio in real time, or Spectral Array Oscillation (SAO), in which it uses stored arrays of spectra to resynthesize sounds. We'll cover these modes in greater detail in a bit.
It's important to note here that Spectraphon is Make Noise's most complex digital module to date. It has a ton of inputs and outputs, a ton of front panel controls, and a ton of visual feedback. This was enabled in part through a collaboration between Make Noise designer Tony Rolando and Jeff Snyder of Snyderphonics. Based on an ARM Cortex-H7 MCU running at 480MHz with plenty of SDRAM and FLASH memory, a 5V audio CODEC with high signal to noise ratio, and DC-coupled I/O, the Spectraphon's DSP hardware not only enables considerably higher dynamic range and signal to noise than prior designs, but also provides the possibility for a large number of low-noise audio I/O. That said, let's get back to talking about how it works from a user perspective by taking a look at its front panel.
Each of Spectraphon's oscillators is nearly identical to one another; so, let's take a look to see what features they offer. Each oscillator has four outputs: a dedicated sine output, a Sub/CV output, and outputs for Odd and Even partials—summed to the Odd partial outputs when the Even partials outputs are unpatched. The Sub/CV output is assignable using a combination button press. It can produce a stepped random voltage, smooth random voltage, or triangle LFO. When in SAM mode, it can also produce an envelope follower signal based on the incoming audio's level; when in SAO mode, it produces a suboscillator tone—a saturated sine wave on one side, and a saw wave on the other. When the Sub/CV outputs are set to produce control voltages, the rate of the CV is determined via the Clock input and shift button, which operates like a tap tempo control. Each of the two oscillators also features an external input at the top of the panel, whose functionality changes depending on the current mode selection. Each oscillator also features a single 1V/octave pitch CV input, a large coarse tuning knob, and a small fine tuning knob.
Spectraphon, of course, also offers a variety of ways of altering the timbre of the oscillator at the Odd and Even harmonic outputs. The most dramatic of these in many situations is the Partials control, which alters the amplitude of the partials at the Odd and Even outputs: with Partials at its minimum value, these outputs are silent. As Partials is increased, more and more partials are revealed at these outputs, and the sound gets brighter/more intense: somewhat like the effect of a filter or low pass gate. Partials features a CV input with dedicated attenuverter, so it may even be treated like a pseudo-end-of-voice gate, great for imparting articulation without the need for external LPGs or VCAs.
As with the external signal inputs, the Slide and Focus controls change in function depending on whether you're working in SAM or SAO mode. As such...we'll come back to these in a bit.
Much like in the Buchla 259, the center of the module features a modulation bus for facilitating inter-oscillator modulation. In Spectraphon, this is limited to inter-oscillator frequency modulation—and happily, it will accommodate frequency modulation between each of the oscillators. In fact, there are two FM index controls—one for modulating from side A to side B, and vice versa. There are a few things worth noting here: first of all, the modulation indices get insanely deep—the custom DSP platform at Spectraphon's core allows for high-resolution, high-index, high-frequency FM, and it sounds bonkers. The second thing worth noting is that the FM Bus only affects the Odd and Even harmonic outputs on each side; it has no impact on the sine outputs, nor on the suboscillator outputs. And in fact, because the FM is only calculated on these specific outputs, it's possible to do bi-directional frequency modulation without the chaotic/intense/destabilizing effects of typical cross-modulation (as on the Make Noise DPO, for instance). Originally I saw this as a downside, but it's actually quite useful; and trust me, the FM gets deep enough that you don't exactly need chaotic cross-modulation to get to some truly intense sounds.
The A side's Mod Bus features a dedicated modulation depth knob and accompanying CV input and attenuverter; the B side knob functions as an offset by default, but as an attenuator when external CV is applied. So, dynamic modulation depth is easily achievable both directions. The B side features a button that allows it to pitch follow the A oscillator's tuning knob and CV input, or to hard sync to the A oscillator. The LED window in the B section lights up red or green in order to indicate when the tuning between the oscillators has reached relatively harmonic ratios. Again, otherwise, these oscillators are effectively identical to one another.
At this juncture, though, we need to dive deeper: let's talk about the difference between Spectral Amplitude Modulation and Spectral Array Oscillation.
Spectral Amplitude Modulation

Understanding Spectraphon first requires understanding Spectral Amplitude Modulation mode. When an oscillator in Spectraphon is set to SAM mode, its timbre is derived from an instantaneous analysis of an external sound source at its signal input. The input can accept modular or line level signals, with continuously variable gain. In essence, it analyzes the frequency content of an external sound, and maps that overtone structure onto the oscillator itself—almost as if external sounds are "exciting" a large bank of oscillators, or a resonator. This is the key to how Spectraphon's approach to resynthesis works.

The thing is—the pitch at the output is always determined by the position of the Frequency knob and the 1V/octave CV input; it doesn't attempt to track the pitch of external audio signals at all. So, that begs the question...how the heck does it know how to map the overtone structure of your incoming sound on to the oscillator? How does it decide which overtones go where if it isn't also tracking the external signal's pitch? That's where the Slide control comes in: in effect, it's acting like a hypothetical fundamental around which to analyze the incoming sound. It then determines the relationship between the "Slide" frequency and the frequencies present at the input, and uses that to determine how to construct the oscillator's output overtone structure.
Does that sound insanely confusing? Well, the point is this: the output pitch is always determined by the oscillator tuning knobs, with the overtone structure determined by the signal at the external input. You can then use the Slide control as a sort of continuous formant shift—sliding the overtone mapping to higher and lower parts of the oscillator's spectrum. Depending on how Slide is set, you might wind up with a sound that is very similar to the input; or, alternatively, you might get something much more peculiar. This is all key to Spectraphon's vocoder-like behavior: it'll produce a sound that tracks the spectral content of incoming tones, but with a pitch completely independent from the input. In fact, Spectraphon works quite well for Laurie Anderson-style vocal harmonies, or any scenario in which you want to use an external sound source to "excite" a more synthetic style tone.
The Focus control is a bit more difficult to explain: it acts almost like a spectral blurring or "ringing" effect, causing a tendency for Spectraphon to lag behind external input, and for excited overtones to "ring" longer. You can suddenly turn Focus up to perform a sort of spectral Freeze; modulating Focus as you perform can be used to similar effect.
It's also worth noting that inter-oscillator FM and sync work in both SAM and SAO modes—so it's possible to frequency modulate the instantaneously resynthesized tones, or to hard sync your vocoded voice, or any number of other peculiar and dang-near-unheard-of tricks. It sounds quite bizarre. Another nice thing to consider is that you could pipe any sound you like into spectraphon—drums, voice, other instruments, other synthesizer sounds. The end result will be a synthesized tone with a highly animated audio spectrum, with tuning dependent on its own pitch knob and pitch CV. This could be quite an interesting way to create melodic or harmonic backing for other sounds, or simple to create timbres with rich internal movement.
Spectral Array Oscillation
Let's say, though, that you don't want to have to constantly send sound into Spectraphon's input in order to create sound. That's what Spectral Array Oscillation mode is all about. When in SAM mode, you can perform an analysis of an external sound source and store it into an internal "Array." An Array is comprised of over 1000 Spectra; Spectra are "snapshots" of a sound's spectrum, each captured one after another. Spectraphon can store up to sixteen Arrays for each side of the module; these may be selected using a button combination, with currently selected Array displayed via the four LEDs behind the rad dual sine-wave-looking display in the center of the module. Arrays are typically created by analyzing the incoming sound once every millisecond or so, but you may send a clock into the clock input while creating an Array in order to work with sounds that need more than a second to unfold.

So, what can you do with an Array? When you switch the oscillator in question to SAO mode, you suddenly have the ability to use the Spectra in the Arrays to define the timbre of the oscillator. Suddenly, the function of the Slide and Focus controls changes: they become a way of "scrubbing" through the Array, allowing you to smoothly scan through the captured sound to create everything from smooth reversed tones to stuttering, sliding, jittery re-constructions of the source sound. It's important to note that this isn't using audio recordings or samples (like on a Morphagene, for instance)—it's simply accessing a bank of analyses of the original audio and allowing you to smoothly interpolate or immediately jump between different parts of the original sound. Slide acts somewhat like a "coarse" scrub control, with Focus scrubbing through smaller segments of the Array. In this mode, the Clock input and shift buttons can be used to advance through the Array, one Spectrum at a time.
The signal inputs and corresponding controls also change in function in SAO mode. The A-In and B-In knobs suddenly act as frequency offsets for the sound's Even partials, offsetting them anywhere up to an octave above their original frequency. This means that you can do everything from bizarre chorusing and spectrally-based stereo widening tricks all the way to two note harmonies on each side; if you play your cards right and set all the knobs accordingly, Spectraphon could even create four-note chords using both oscillators in SAO mode. The input jacks act as CV inputs for the offset on the Even harmonic outputs; when an external CV or audio source is plugged in, the corresponding knob acts as an attenuator for the incoming modulation. You can sequence the Even outputs; you can FM the Even outputs; anything goes.
Spectraphon In Review
So, this article has left us with a lot of theory, and a lot of explanation. The simple fact is that, at the moment, there aren't a lot of audio examples out there of Spectraphon or how it works—but with Superbooth underway, we anticipate that we'll see and hear a lot more from it in the coming days. For now, though, we have to use our imaginations: what would it be like to play a guitar into Spectraphon? What if you used both sides as vocoders with separate vocalists? What if you used one side in SAO mode, and passed it through the other in SAM mode? At the moment, these questions have no answer—but we're quite excited to see and hear how people choose to use it once it's out in the wild. For now, I'll have to remain satisfied with my imagination—and my imagination is running wild.
At the moment, suffice it to say that Spectraphon is an engineering marvel. Tony Rolando and Jeff Snyder's new DSP platform has enabled Make Noise and Tom Erbe to embark on what I firmly believe is their most ambitious design expedition to date. It's a huge digital mode with a ton of outputs and inputs and insanely high sound quality. It takes on synthesis concepts seldom approached in hardware. It presents novel, creative solutions to the problems presented by additive synthesis, providing a unique way of taking control of this severely under-utilized synthesis technique. Simultaneously, it pays deeply thoughtful and respectful tribute to some of the most interesting designs made by Don Buchla, himself one of the most interesting instrument designers of all time.
All in all? Spectraphon is a positive bundle of interesting ideas and interesting sounds, and I'm downright giddy to consider what sort of music will come from it.