A portrait of a generic oscillator

Oscillators vary greatly by design as a result of historic strive of inventors to create units capable of generating new sonic timbres; however there are several underlying parameters that are shared across the spectrum. Primarily these include knobs or sliders for setting coarse and fine tuning, supported by the v/8 (volts per octave) control input; options for waveform selection with a dedicated control over the duty cycle parameter if a square wave is on the menu; an input for frequency modulation (FM), which in the best cases also allows for switchable linear or exponential response. The commonly utilized building block waveforms that various manufacturers agreed upon decades ago are sine, sawtooth, square and triangle.

In the modern days sonic adventurers are not limited to the analog oscillator format with its more or less defined palette of waveforms. Digital technology not only helped stabilize the tuning of the oscillators, but also opened up other possibilities with endless amounts of complex waveshapes, easily achievable through such synthesis techniques as wavetable, wavelet, vector, VOSIM, and more. More on this later.

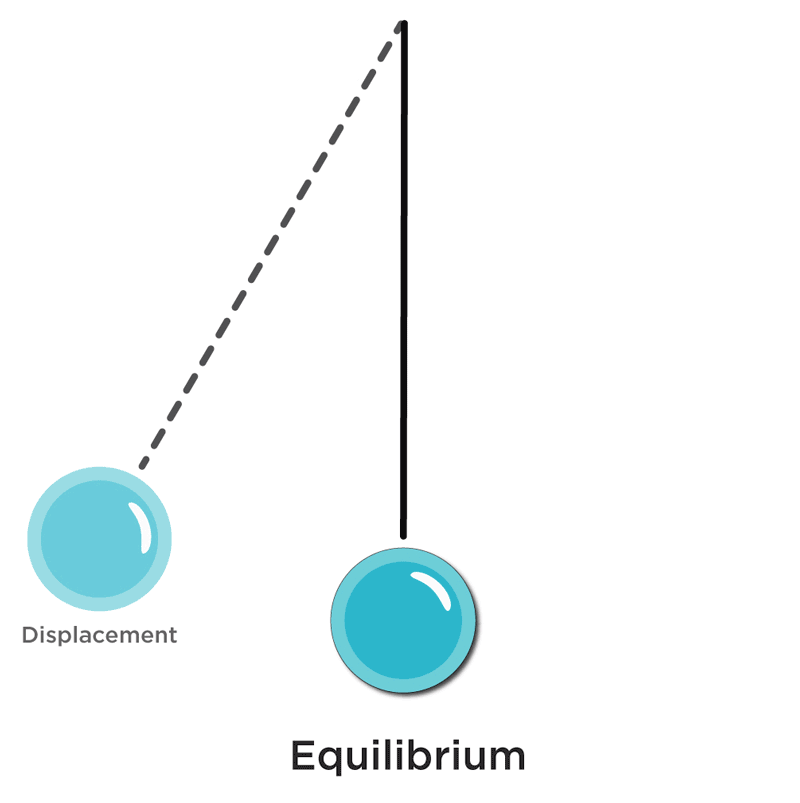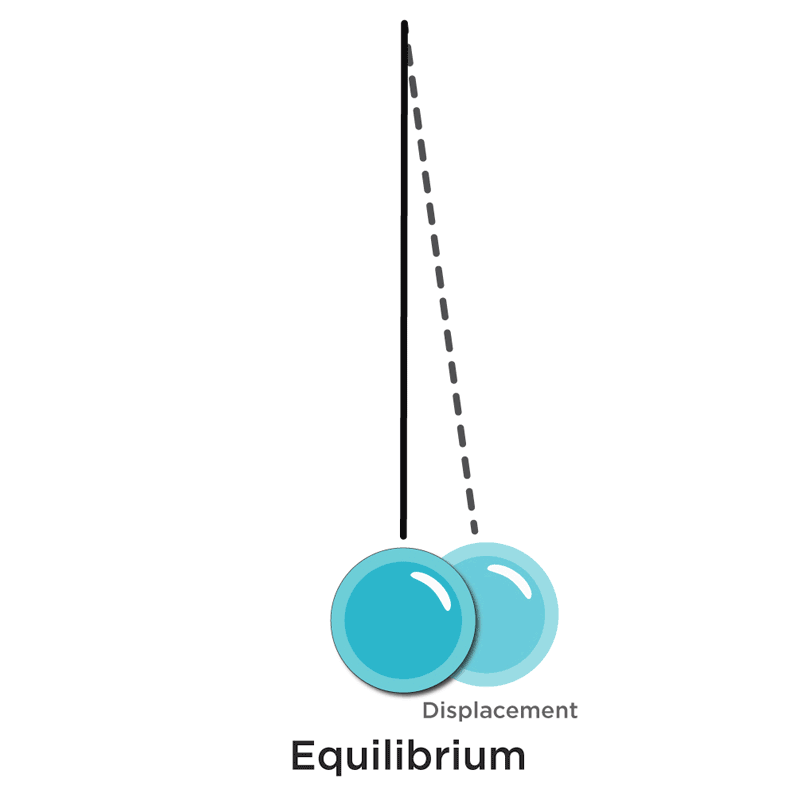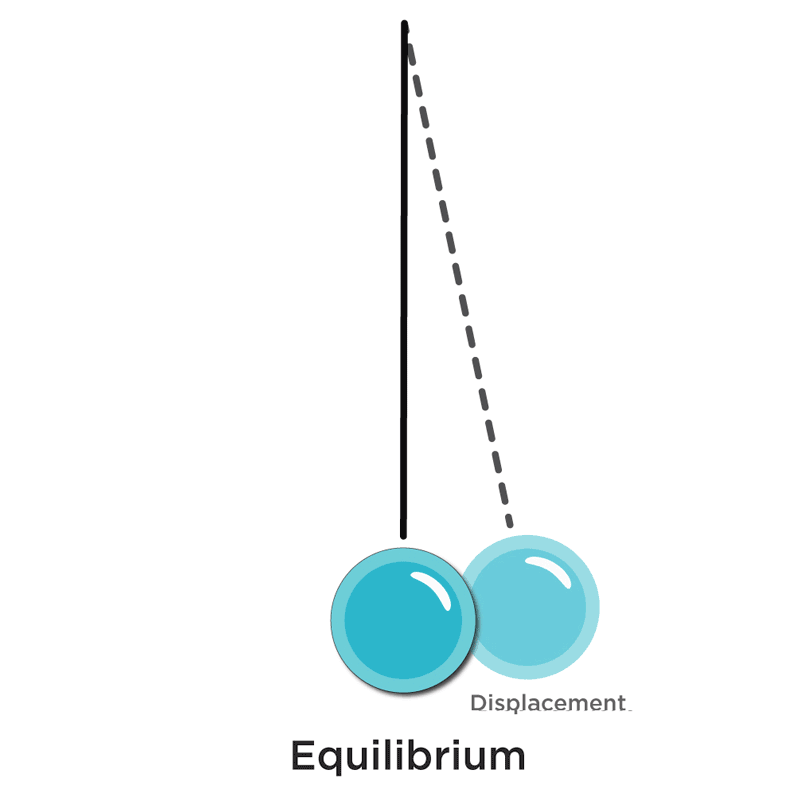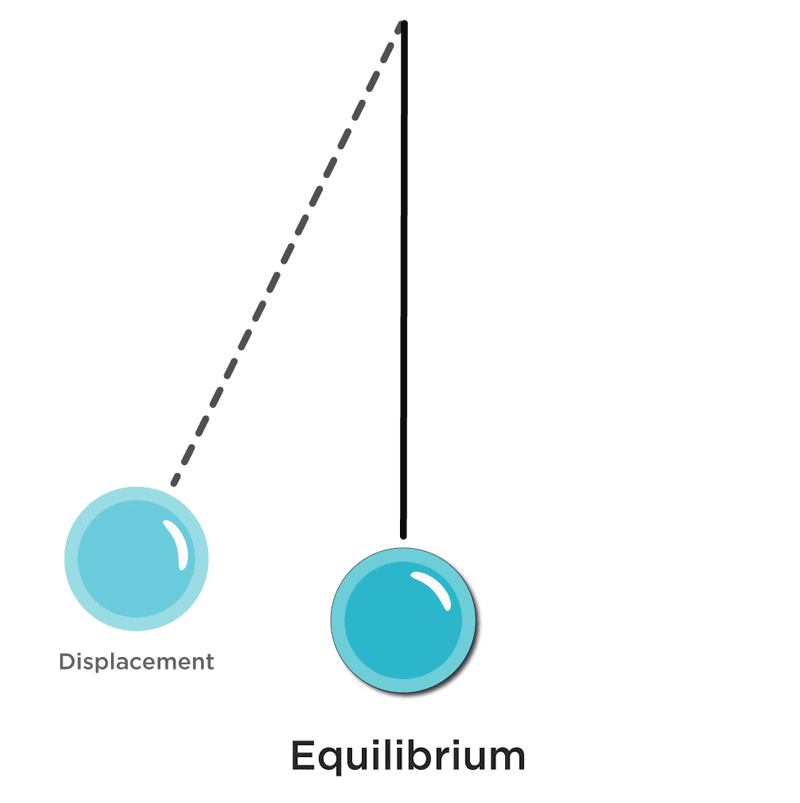
To understand the general principle of operation of any oscillator and just to define what they are, we need to revisit a physics principle known as a simple harmonic motion. SHM is described as a distinctly unique type of periodic motion (or oscillation), where the restoring force is equivalent to the force of original displacement, and it is aimed in the direction opposite from the direction of the initial dislocation. One example often applied here is that of a pendulum. Imagine a weight suspended on a string. When it is undisturbed, it remains at its equilibrium position. If we were to lift it towards one side and let go, the weight would start swinging back and forth going through cycles of acceleration and deceleration, trying to restore to its original resting position. A wave fluctuating between positive and negative voltages is not all that different from this swinging pendulum.

Arp 2500 was unique in utilizing both triangular and sawtooth VCO cores

Let’s talk about how analog oscillators produce the set of waveforms mentioned above. Contrary to a common misconception, the waveforms are not produced independently of each other, but rather derived from one main waveform, known as the oscillator core. There are two waveforms that are primarily used as a core, which are triangle and sawtooth. The two differ in the methods of deriving other shapes from them, each having its strengths and weaknesses. Sawtooth core is simpler in implementation, and thus it is generally more wide spread.

Buchla’s early 158 Dual Sine-Sawtooth Generator, for instance, employed a sawtooth core. Triangle core oscillators are a bit more demanding from an engineering standpoint, yet they are reported to produce better, more stable results when subjected to frequency modulation. A common historic example of the triangular core oscillator is Curtis CEM3340 chip found in Roland SH-101, Oberheim Ob-Xa, Moog Memorymoog, etc. A unique case of a VCO utilizing both triangular and sawtooth cores is the one found in the Arp 2500. It was achieved by tying both cores to a single reset mechanism.

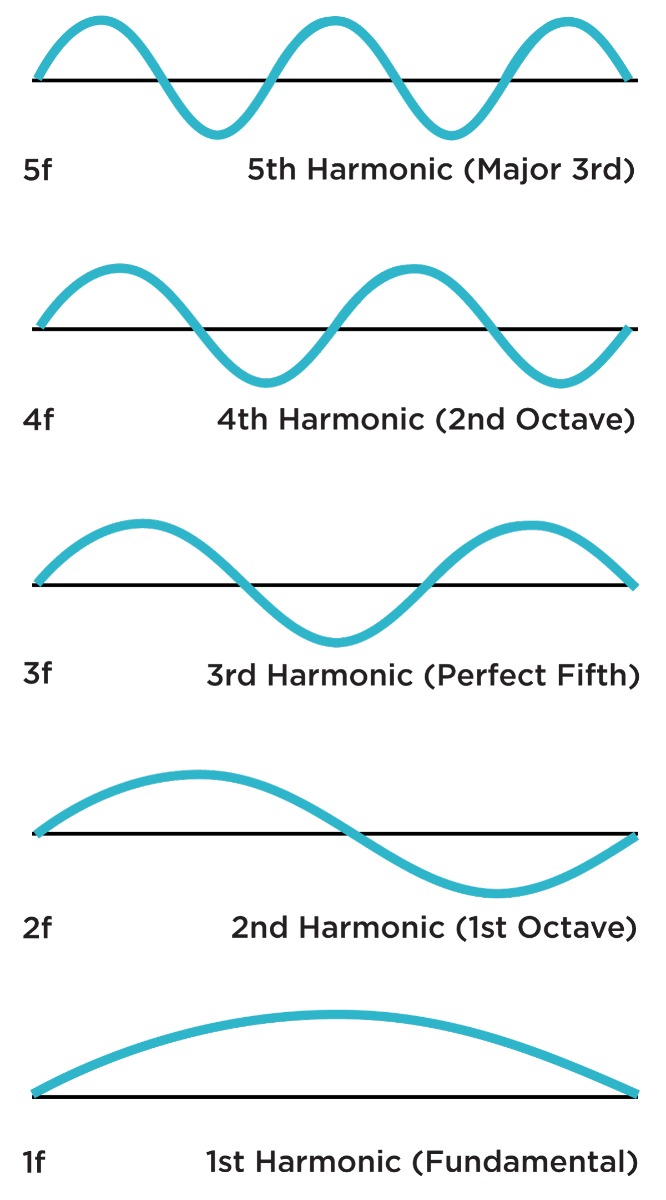
The symbols representing traditional waveform shapes are not arbitrary. They act as a reductive portrayal of sonic timbers, indicating mathematical relationships between the fundamental frequency of a tone, its overtones and their individual amplitude.

Let’s clarify the terms a bit. Fundamental is considered to be the loudest frequency in the spectrum and it is equivalent to our perceived pitch of a tone. Overtones are all frequencies in a spectrum above the fundamental. Together, a fundamental and its overtones are called partials. Harmonic partials (or commonly harmonics) are integer multiples of the fundamental, e.g. if the fundamental frequency is ƒ, then the first harmonic is 1ƒ (hint: it is the fundamental itself), and 2ƒ, the second harmonic partial, is twice the base frequency; consequently 3ƒ is the third harmonics and it is a perfect fifth apart from the 2nd harmonic, etc. Amplitude variance between the fundamental and its various partials is what makes you tell the difference between the sound of a guitar and a piano. Synthesizers give us a whole lot of control over shaping and modifying spectral content of sounds.

By spectrum we define a group or series of frequencies that are present in the sound. Applying this to the traditional waveshapes, we know that a pure sine wave has no overtones. Triangular and square waves contain only odd harmonics, though at significantly different amplitude proportions, which results in only slight tonal richness of the former, and extreme sonic brightness of the latter. Sawtooth wave, on the contrary, is made up of both odd and even harmonics, a spectral fingerprint not too far off from that of a violin.

Additive synthesis is a method of constructing new timbres and complex waveforms through mixing together simple components like sine waves in different proportions of frequencies and amplitudes. This means that if we know the correct amplitude relationships between the fundamental and harmonic partials of any given sound, be so an acoustic sound of clarinet or a rich waveshape like sawtooth, we can technically recreate it using several sine wave oscillators. Buchla’s 148 Harmonic Generator and its modern counterpart Verbos’ Harmonic Oscillator are perfect examples of the additive synthesis units capable of generating intricate waves through dynamic mixing of pure tones.

Buchla's dual oscillator model 158 was created with an idea of one oscillator being used to modulate the frequency of the other

We know by now that one of the key features of synthesis is modulation. Depending on what parameter the modulation is applied to significantly alters the resulting sound. One of the most common modulation techniques directly related to oscillators is frequency modulation or FM. It works by sending an output of arbitrary voltage source, such as a LFO, an oscillator or an envelope generator to the frequency input of the primary oscillator causing controllable fluctuations of the perceived pitch.

When LFO or audio rate oscillator is applied a vibrato effect is achieved at slower rates, while faster modulation is capable of transcending the original sound towards new timbral territories. When envelope is applied, the oscillator output can be shaped to provide anything from glissando effects to percussive material. Frequency modulation is so common that you will often find a dedicated FM input, sometimes with an additional attenuator for controlling the modulation amount, on many oscillators.

If we take a look at the classic Moog 901 oscillator originally found in the early Moog synthesizer systems, we will find a very familiar set of controls and outputs that is used in synthesizer designs to this day. Essentially 901 combines the two smaller siblings, 901a and 901b, under one panel. As one would expect, it offers simultaneous fixed level output of the four traditional waveforms: sine, sawtooth, triangular and pulse (square).

Unique to this particular oscillator is an optional variable level output of the individual waveforms, rendering it especially capable of additive wave sculpting. You will also find controls for frequency range selection, pulse width, fixed control voltage and fine tuning control for pitch, as well as three inputs for external control voltage.

This oscillator format, with only slight alterations, became a foremost design format not only for future Moog synthesizers, including the legendary Model D, but also for many other machines from various manufacturers, such as Arp 2600, Korg MS-20, Roland’s Jupiter 8, and others. In the Eurorarck realm there is also no shortage of Moog format oscillators, namely Intellijel Dixie II and II+, AJH Minimod VCO, Doepfer A-110-1, Grp P02 VCO, and so on.

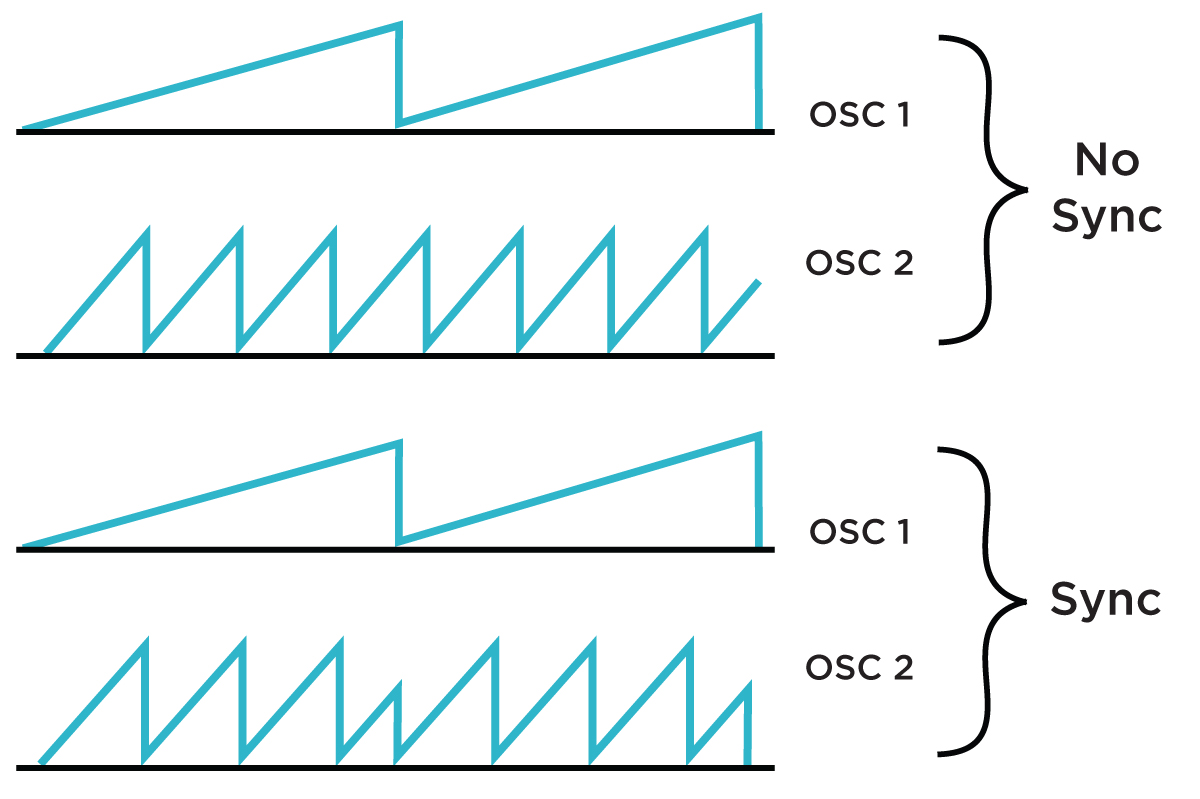
One more aspect that we need to touch upon here, before moving forward is synchronization. Tuning of analog oscillators has always been a very painstaking process, especially when you have a few of them in your system. Essentially, synchronization allows two or more oscillators to stay in tune with each other through a predetermined interval relationship. One is designated to act as a master and the other one as a slave. The process of synchronization involves sending the pulse wave of the master oscillator to the sync (synch, lock, capture) input of the slave, thus forcing the latter to follow the changes in the frequency rate of the former.

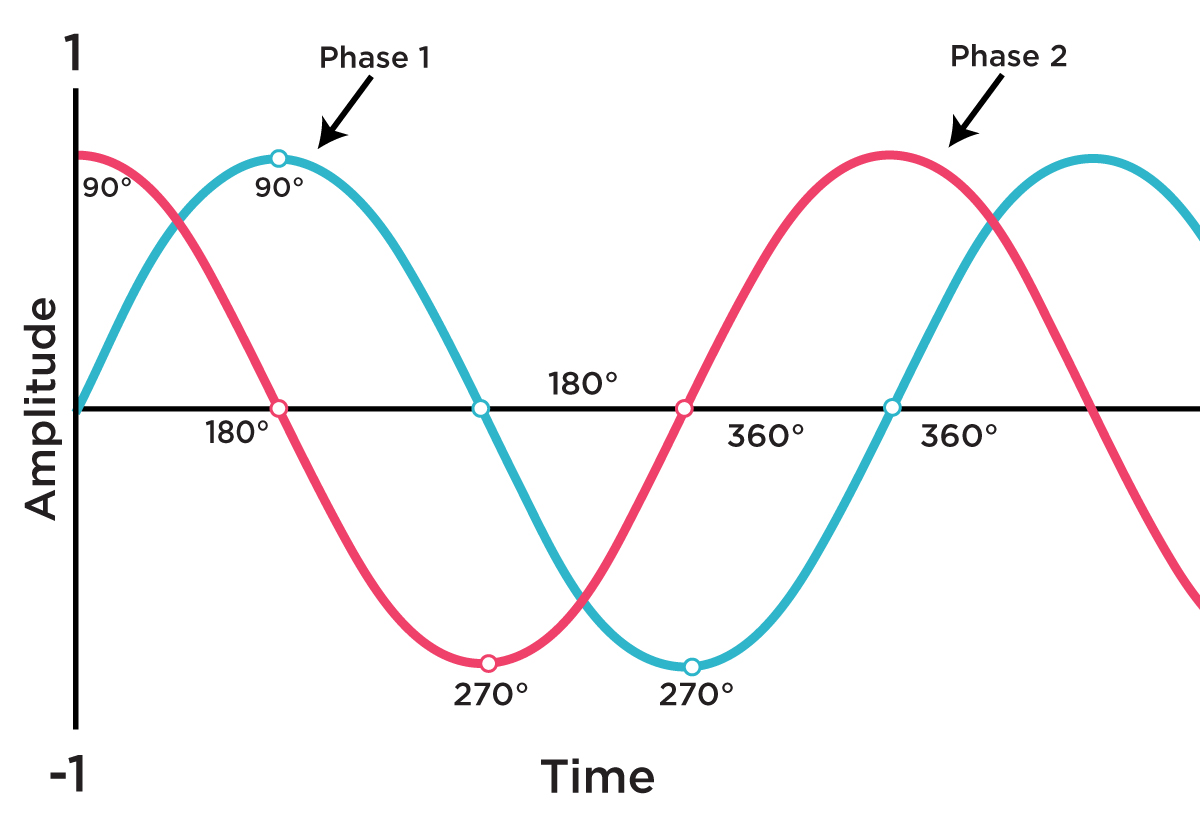
There are two primary terms associated with the oscillator synchronization: hard sync and soft sync. Hard sync forces the slave oscillator to reset its phase to zero every time the master oscillator restarts its cycle. By phase we understand a fundamental parameter of sound that determines the position in time within a given cycle of a waveform.

Soft sync is trickier, as it entails multiple ways of implementation. One application would involve the slave oscillator to invert its waveshape every time the master source returns to zero. The other explanation that we came across deals with probabilistic setting of the slave oscillator, e.g. 50% soft sync would render the slave oscillator to reset its phase to zero volts only half of the time the master oscillator restarts its cycle. There are potentially other ways for the realization of soft syncing, but we won’t go into them this time.

Some of the early implementations include such iconic machines as Roland Juno 106 and Juno 60 and Korg Poly-61. DCOs were helpful in solving the tuning issues of analog synthesizers, but they were limited to the same traditional waveform shapes so a change was on the way.

With synthesis techniques like the aforementioned wavetables, the scope of potential waveforms is truly limitless, enabling any sound (and sometimes not even sound) source to be transformed into a periodic waveform. Originally wavetable synthesis was developed by the Wolfgang Palm in the late 1970s for his innovative PPG synthesizer. The method was quickly picked by Waldorf Music, Ensoniq and eventually Access for the wide breadth of their products. In principle, the method involves a periodic reproduction of any single cycle waveform.

The wavetable itself represents a bank of waveforms that can be scanned through manually or via modulation. Often synthesizers employing this technique come with a wide range of selectable and scannable waveforms, some even allowing users to load their own wavetables into the memory of a synthesizer. Smoothness of scanning between the waveforms is achieved, though a technique called digital interpolation. It is also not uncommon for wavetables to simulate traditional waveforms to mimic the results of analog synthesis.

Not too dissimilar, but very often confused with wavetables is a sample-based synthesis. In this case the waveform is not limited to a single cycle, technically rendering recorded sound of any length to serve as source material for synthesis. Several granular synthesis techniques can be safely placed in this category.

Lastly we will look at the digital waveguide based oscillators. Waveguides are bi-directional delay lines used as a method of computational modeling of acoustic phenomena. These are usually employed as sources in the physical modeling synthesis as a strategy to simulate behavior of physical objects like strings, tubes, membranes, etc. Physical modeling synthesis is quite a deep subject in itself and we will get back to the this technique in a dedicated future articles.